题目内容
20.如图.有一座抛物线形拱桥.在正常水位时桥下水面AB的宽度为20m.这时.拱高(点O到AB的距离)为4m.(1)你能求出在图(a)的坐标系中.抛物线的函数表达式吗?
(2)如果将直角坐标系建成如图(b)所示,抛物线的形状、表达式有变化吗?
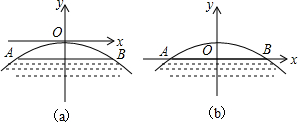
分析 (1)由函数图象可设该抛物线的解析式是y=ax2,再结合图象,只需把(10,-4)代入求出a的值即可;
(2)由函数图象可设该抛物线的解析式是y=ax2+c,再结合图象,只需把(10,0),(0,4)代入求出a、c的值即可.
解答 解:(1)设该抛物线的解析式是y=ax2,
由图象知,点(10,-4)在函数图象上,代入得:
100a=-4,
a=-$\frac{1}{25}$.
∴该抛物线的解析式是y=-$\frac{1}{25}$x2;
(2)设该抛物线的解析式是y=ax2+c,
由图象知,点(10,0)(0,4)在函数图象上,代入得:
$\left\{\begin{array}{l}{100a+c=0}\\{c=4}\end{array}\right.$,
解得:a=-$\frac{1}{25}$,c=4.
∴该抛物线的解析式是y=-$\frac{1}{25}$x2+4,
与(1)抛物线比较,形状不变、表达式有变化.
点评 本题考查了二次函数在实际问题中的应用,能够熟练运用待定系数法求得二次函数的解析式是此题的考查点.

练习册系列答案
相关题目
5.下列说法正确的是( )
①正方体的截面可以是等边三角形,②正方体不可能截出七边形,③用一个平面截正方体,当这个平面与四个平面相交时,所得的截面一定是正方形,④正方体的截面中最多的是六边形.
①正方体的截面可以是等边三角形,②正方体不可能截出七边形,③用一个平面截正方体,当这个平面与四个平面相交时,所得的截面一定是正方形,④正方体的截面中最多的是六边形.
| A. | ①②③④ | B. | ①②③ | C. | ①③④ | D. | ①②④ |
 如图,已知AB∥CD∥EF,AF与BE交于O点,若AF=9,BO=2,OC=1,CE=4,求DF和OD的长.
如图,已知AB∥CD∥EF,AF与BE交于O点,若AF=9,BO=2,OC=1,CE=4,求DF和OD的长.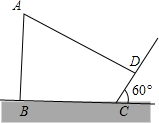 小刚在利用阳光下的影子测量大树AB的高度时,大树的影子恰好落在了山坡坡面CD和地面BC上,他用2m长的竹竿测得CD=4m,BC=10m,用量角器测得斜坡CD与地面BC成60°角,如图所示,且测得此时长2m的竹竿的影长为1m,求大树AB的高度.(结果可保留根号)
小刚在利用阳光下的影子测量大树AB的高度时,大树的影子恰好落在了山坡坡面CD和地面BC上,他用2m长的竹竿测得CD=4m,BC=10m,用量角器测得斜坡CD与地面BC成60°角,如图所示,且测得此时长2m的竹竿的影长为1m,求大树AB的高度.(结果可保留根号)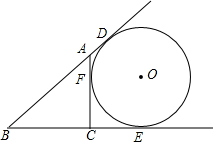 如图所示,已知AC⊥BC,BC=4,AC=3,⊙O与直线AB,BC,CA都相切,切点分别为D,E,F.求⊙O的半径.
如图所示,已知AC⊥BC,BC=4,AC=3,⊙O与直线AB,BC,CA都相切,切点分别为D,E,F.求⊙O的半径.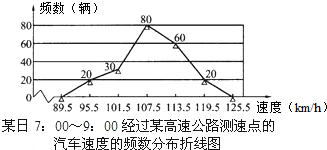 超速行驶是交通事故频发的主要原因之一,交警部门统计某日7:00-9:00经过高速公路某测速点的汽车的速度,得到如下频数分布折线图,若该路段汽车限速110km/h,则超速行驶的汽车有( )
超速行驶是交通事故频发的主要原因之一,交警部门统计某日7:00-9:00经过高速公路某测速点的汽车的速度,得到如下频数分布折线图,若该路段汽车限速110km/h,则超速行驶的汽车有( )