题目内容
对自然数列1,2,3,4,5,6…进行淘汰,淘汰的原则是:凡不能表示为两个合数之和的自然数均被淘汰,如:“1”应被淘汰;但12可以写成两个合数8与4的和,不应被淘汰.被保留下来的数按从小到大的顺序排列,则第2004个数是( )
| A、2015 | B、2014 |
| C、2013 | D、2012 |
考点:规律型:数字的变化类
专题:
分析:把自然数分为奇数和偶数两类讨论,能表示成两个偶合数之和的最小自然数是:4+4=8;因为大于8的偶数比8大的部分是偶数,将大的部分的偶数加到4上一定是合数;所以大于8的偶数都可以表示为两个合数之和的自然数,可以被保留下来;那么自然数列就只剩下了奇数,奇数能表示成两个合数之和的最小自然数是:4+9=13,又根据数的奇偶性,任何大于13的奇数与13的差一定是偶数,将差偶数加到4上一定是合数,所以大于13的奇数都可以表示为两个合数之和的自然数,可以被保留下来;这样大于8的偶数和大于13的奇数都需要被保留下来;反之,小于8的偶数和小于13的奇数都需要被淘汰:即1、2、3、4、5、6、7、9、11;那么被保留下来的数是:8、10、12、13、14、15、16、…然后根据等差数列即可求出第2004个数即可.
解答:解:最小的偶合数是4,最小的,奇合数是9;
能表示成两个偶合数之和的最小自然数是:4+4=8;所以在大于8的偶数M都比8大2N,将增加的2N加到4上一定是合数即:M=(4+2N)+4,所以大于8的偶数都可以表示为两个合数之和的自然数,可以被保留下来;
那么自然数列就只剩下了奇数,下面我们就研究奇数:
奇数如果能表示成两个合数之和,根据数的奇偶性,说明这两个合数必定是一奇一偶,
那么奇数能表示成两个合数之和的最小自然数是:4+9=13,又根据数的奇偶性,任何大于13的奇数m与13的差一定是偶数2N,将2N加到4上一定是合数即:m=(4+2N)+9,所以大于13的奇数都可以表示为两个合数之和的自然数,可以被保留下来;
所以小于8的偶数和小于13的奇数都需要被淘汰:即1、2、3、4、5、6、7、9、11;
那么被保留下来的数是:8、10、12、13、14、15、16、…
从12开始是一个等差数列,2004-2=2002,则第2004个数是:a2004=12+(2002-1)×1=2013.
故选:C.
能表示成两个偶合数之和的最小自然数是:4+4=8;所以在大于8的偶数M都比8大2N,将增加的2N加到4上一定是合数即:M=(4+2N)+4,所以大于8的偶数都可以表示为两个合数之和的自然数,可以被保留下来;
那么自然数列就只剩下了奇数,下面我们就研究奇数:
奇数如果能表示成两个合数之和,根据数的奇偶性,说明这两个合数必定是一奇一偶,
那么奇数能表示成两个合数之和的最小自然数是:4+9=13,又根据数的奇偶性,任何大于13的奇数m与13的差一定是偶数2N,将2N加到4上一定是合数即:m=(4+2N)+9,所以大于13的奇数都可以表示为两个合数之和的自然数,可以被保留下来;
所以小于8的偶数和小于13的奇数都需要被淘汰:即1、2、3、4、5、6、7、9、11;
那么被保留下来的数是:8、10、12、13、14、15、16、…
从12开始是一个等差数列,2004-2=2002,则第2004个数是:a2004=12+(2002-1)×1=2013.
故选:C.
点评:此题考查数字的变化规律,找出数字之间的运算规律,利用规律,解决问题.

练习册系列答案
相关题目
从一个n边形的同一个顶点出发,分别连接这个顶点与其余各顶点,若把这个多边形分割成10个三角形,则n的值是( )
| A、11 | B、12 | C、13 | D、14 |
在实数
,
,
,π,-2,
,
,
,
,0中,无理数的个数是( )
| 3 | 9 |
| 1 |
| 3 |
| 7 |
| 2 |
|
| 3 | 8 |
|
| A、4 | B、5 | C、6 | D、7 |
已知(a+b)2=m,(a-b)2=n,则ab等于( )
A、
| ||
B、-
| ||
C、
| ||
D、-
|
 (1)请找出该残片所在圆的圆心位置,其中点A、B、C在圆上(保留画图痕迹,不必写画法);
(1)请找出该残片所在圆的圆心位置,其中点A、B、C在圆上(保留画图痕迹,不必写画法);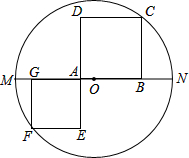 如图,MN是⊙O的直径,MN=6,B是线段ON上一动点,四边形ABCD和AEFG都是正方形,其中点G,A在MN上,点C,F在图上,则正方形ABCD与正方形AEFG的面积和为
如图,MN是⊙O的直径,MN=6,B是线段ON上一动点,四边形ABCD和AEFG都是正方形,其中点G,A在MN上,点C,F在图上,则正方形ABCD与正方形AEFG的面积和为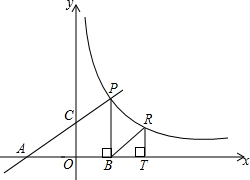 如图,直线y=
如图,直线y= 如图,在沱江河边P处,望对岸有两棵相隔100米的大树,左边一棵在东北方向上,右边一棵在北偏东60°方向上,请帮忙计算沱江河宽.(结果保留根号)
如图,在沱江河边P处,望对岸有两棵相隔100米的大树,左边一棵在东北方向上,右边一棵在北偏东60°方向上,请帮忙计算沱江河宽.(结果保留根号)