题目内容
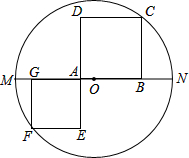 如图,MN是⊙O的直径,MN=6,B是线段ON上一动点,四边形ABCD和AEFG都是正方形,其中点G,A在MN上,点C,F在图上,则正方形ABCD与正方形AEFG的面积和为
如图,MN是⊙O的直径,MN=6,B是线段ON上一动点,四边形ABCD和AEFG都是正方形,其中点G,A在MN上,点C,F在图上,则正方形ABCD与正方形AEFG的面积和为考点:勾股定理,圆的认识
专题:
分析:客观题可采用特殊方法,因为B是ON上任意一点,故可取特殊位置,即可取O、C、F三点在一条线上时,容易求得两正方形的面积和.
解答: 解:
解:
∵B为线段ON上的任意点,
∴可取O、C、F三点在一条线上的位置,
如图,则OC=OF=3,
∴S正方形ABCD=S正方形AEFG=
×32=
,
∴S正方形ABCD+S正方形AEFG=9,
故答案为:9.
 解:
解:∵B为线段ON上的任意点,
∴可取O、C、F三点在一条线上的位置,
如图,则OC=OF=3,
∴S正方形ABCD=S正方形AEFG=
| 1 |
| 2 |
| 9 |
| 2 |
∴S正方形ABCD+S正方形AEFG=9,
故答案为:9.
点评:本题主要考查正方形的性质及圆的特征,由于是客观题,故可借助B点的任意性采用特殊位置法来解,注意正方形面积的计算.

练习册系列答案
相关题目
一个数的绝对值等于13,这个数是( )
| A、13 | ||
| B、-13 | ||
| C、±13 | ||
D、
|
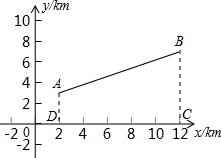 去冬今春,济宁市遭遇了200年不遇的大旱,某乡镇为了解决抗旱问题,要在某河道建一座水泵站,分别向河的同一侧张村A和李村B送水.经实地勘查后,工程人员设计图纸时,以河道上的大桥O为坐标原点,以河道所在的直线为x轴建立直角坐标系(如图).两村的坐标分别为A(2,3),B(12,7).
去冬今春,济宁市遭遇了200年不遇的大旱,某乡镇为了解决抗旱问题,要在某河道建一座水泵站,分别向河的同一侧张村A和李村B送水.经实地勘查后,工程人员设计图纸时,以河道上的大桥O为坐标原点,以河道所在的直线为x轴建立直角坐标系(如图).两村的坐标分别为A(2,3),B(12,7).