题目内容
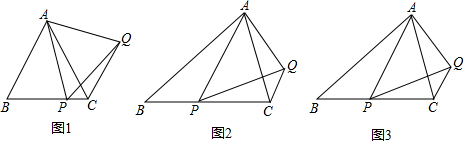
(1)如图1,在等边△ABC中,点P是BC上的任意一点(不含端点B、C),连结AP,以AP为边作等边△APQ,连结CQ.求证:∠ABC=∠ACQ.
(2)如图2,在等腰△ABC中,BA=BC,点P是BC上的任意一点(不含端点B、C),连结AP,以AP为边作等腰△APQ,使顶角∠APQ=∠ABC.连结CQ.试探究∠ABC与∠ACQ的数量关系,并说明理由.
(3)如图3,在△ABC中,点P是BC上的任意一点(不含端点B、C),连结AP,以AP为边作△APQ,使∠APQ=∠B,连结CQ.若要使∠ACQ=∠ABC一定成立,则△APQ与△ABC之间必须具备什么关系?
(2)如图2,在等腰△ABC中,BA=BC,点P是BC上的任意一点(不含端点B、C),连结AP,以AP为边作等腰△APQ,使顶角∠APQ=∠ABC.连结CQ.试探究∠ABC与∠ACQ的数量关系,并说明理由.
(3)如图3,在△ABC中,点P是BC上的任意一点(不含端点B、C),连结AP,以AP为边作△APQ,使∠APQ=∠B,连结CQ.若要使∠ACQ=∠ABC一定成立,则△APQ与△ABC之间必须具备什么关系?

考点:全等三角形的判定与性质,等边三角形的性质
专题:
分析:(1)根据等边三角形的性质,可得AB=AC,AP=AQ,∠BAC=∠PAQ=60°,进而得到∠BAP=∠CAQ,再利用SAS可证明△BAP≌△CAQ,继而得出结论;
(2)根据两边对应成比例且夹角相等的两个三角形相似,可得∴△BAP∽△CAQ,根据相似三角形的对应角相等,可得答案;
(3)根据两边对应成比例且夹角相等的两个三角形相似,可得∴△BAP∽△CAQ,根据相似三角形的对应角相等,可得答案.
(2)根据两边对应成比例且夹角相等的两个三角形相似,可得∴△BAP∽△CAQ,根据相似三角形的对应角相等,可得答案;
(3)根据两边对应成比例且夹角相等的两个三角形相似,可得∴△BAP∽△CAQ,根据相似三角形的对应角相等,可得答案.
解答:(1)证明:∵△ABC、△APQ是等边三角形,
∴AB=AC,AP=AQ,∠BAC=∠PAQ=60°,
∴∠BAP=∠CAQ,
在△BAP和△CAQ中,
,
∴△BAP≌△CAQ(SAS),
∴∠ABC=∠ACQ;
(2)解:结论∠ABC=∠ACQ仍成立.
理由如下:
∵AB=BC,PA=PQ,顶角∠ABC=∠APQ,
∴∠BAC=∠PAQ,
△ABC∽△APQ,
∴
=
.
∠BAP=∠BAC-∠PAC,∠CAQ=∠PAQ-∠PAC
∴∠BAP=∠CAQ
=
,
∴△BAP∽△CAQ,
∠ABC=∠ACQ;
(3)若要使∠ACQ=∠ABC一定成立,则△APQ与△ABC之间必须具备BA=BC,顶角∠APQ=∠ABC,PA=PQ.
证明:∵AB=AC,PA=PQ,顶角∠ABC=∠APQ,
∴∠BAC=∠PAQ,
△ABC∽△APQ,
∴
=
.
∠BAP=∠BAC-∠PAC,∠CAQ=∠PAQ-∠PAC
∴∠BAP=∠CAQ
=
,
∴△BAP∽△CAQ,
∠ABC=∠ACQ.
∴AB=AC,AP=AQ,∠BAC=∠PAQ=60°,
∴∠BAP=∠CAQ,
在△BAP和△CAQ中,
|
∴△BAP≌△CAQ(SAS),
∴∠ABC=∠ACQ;
(2)解:结论∠ABC=∠ACQ仍成立.
理由如下:
∵AB=BC,PA=PQ,顶角∠ABC=∠APQ,
∴∠BAC=∠PAQ,
△ABC∽△APQ,
∴
| AB |
| AP |
| AC |
| AQ |
∠BAP=∠BAC-∠PAC,∠CAQ=∠PAQ-∠PAC
∴∠BAP=∠CAQ
| AB |
| AC |
| AP |
| AQ |
∴△BAP∽△CAQ,
∠ABC=∠ACQ;
(3)若要使∠ACQ=∠ABC一定成立,则△APQ与△ABC之间必须具备BA=BC,顶角∠APQ=∠ABC,PA=PQ.
证明:∵AB=AC,PA=PQ,顶角∠ABC=∠APQ,
∴∠BAC=∠PAQ,
△ABC∽△APQ,
∴
| AB |
| AP |
| AC |
| AQ |
∠BAP=∠BAC-∠PAC,∠CAQ=∠PAQ-∠PAC
∴∠BAP=∠CAQ
| AB |
| AC |
| AP |
| AQ |
∴△BAP∽△CAQ,
∠ABC=∠ACQ.
点评:本题主要考查了全等三角形的判定与性质,解答本题的关键是仔细观察图形,找到全等的条件,相似的条件,利用全等的性质、相似三角形的性质证明结论.

练习册系列答案
相关题目