题目内容
17.计算:(1)$\sqrt{27}$×$\sqrt{50}$÷$\sqrt{6}$
(2)($\sqrt{12}+\sqrt{20}$)+($\sqrt{3}-\sqrt{5}$)
(3)$\frac{2}{3}$$\sqrt{9x}$+6$\sqrt{\frac{x}{4}}$
(4)(2$\sqrt{48}$-3$\sqrt{27}$)÷$\sqrt{6}$.
分析 (1)先把二次根式化为最简二次根式,然后利用二次根式的乘除法则运算;
(2)先把二次根式化为最简二次根式,然后合并即可;
(3)先把二次根式化为最简二次根式,然后合并即可;
(4)先把括号内的二次根式化为最简二次根式,然后合并后进行二次根式的除法运算.
解答 解:(1)原式=3$\sqrt{3}$×5$\sqrt{2}$÷$\sqrt{6}$
=15;
(2)原式=2$\sqrt{3}$+2$\sqrt{5}$+$\sqrt{3}$-$\sqrt{5}$
=3$\sqrt{3}$+$\sqrt{5}$;
(3)原式=2$\sqrt{x}$+3$\sqrt{x}$
=5$\sqrt{x}$;
(4)原式=(8$\sqrt{3}$-9$\sqrt{3}$)÷$\sqrt{6}$
=-$\sqrt{3}$÷$\sqrt{6}$
=-$\frac{\sqrt{2}}{2}$.
点评 本题考查了二次根式的混合运算:先把二次根式化为最简二次根式,然后进行二次根式的乘除运算,再合并即可.在二次根式的混合运算中,如能结合题目特点,灵活运用二次根式的性质,选择恰当的解题途径,往往能事半功倍.

练习册系列答案
 天天向上口算本系列答案
天天向上口算本系列答案
相关题目
12.已知水银体温计的读数y(℃)与水银柱的长度x(cm)之间是一次函数关系,现有一支水银体温计,其部分刻度线不清晰(如图),表中记录的是该体温计部分清晰刻度线及其对应水银柱的长度.
(1)求y关于x的函数关系式(不需要写出函数自变量x的取值范围);
(2)用该体温计测体温时,水银柱的长度为6.0cm,求此时体温计的读数.

| 水银柱的长度x(cm) | 4.0 | … | 8.0 | 9.6 |
| 体温计的度数y(℃) | 35.0 | … | 40.0 | 42.0 |
(2)用该体温计测体温时,水银柱的长度为6.0cm,求此时体温计的读数.
9.若不等式组$\left\{\begin{array}{l}{2x-1>3}\\{x≤a}\end{array}\right.$的整数解共有三个,则a的取值范围是( )
| A. | 5≤a<6 | B. | 5<a≤6 | C. | 5<a<6 | D. | 5≤a≤6 |
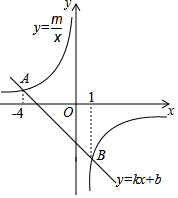 如图,一次函数y=kx+b与反比例函数y=$\frac{m}{x}$的图象交于A、B两点,其横坐标-4、1,则关于x的不等式$\frac{m}{x}$>kx+b的解集为-4<x<0或x>1.
如图,一次函数y=kx+b与反比例函数y=$\frac{m}{x}$的图象交于A、B两点,其横坐标-4、1,则关于x的不等式$\frac{m}{x}$>kx+b的解集为-4<x<0或x>1.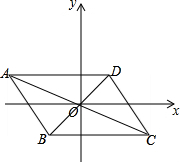 如图,已知点A(-4,2)、B(-1,-2),平行四边形ABCD的对角线交于坐标原点O.
如图,已知点A(-4,2)、B(-1,-2),平行四边形ABCD的对角线交于坐标原点O.