题目内容
6.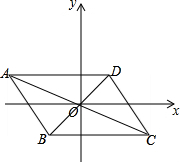 如图,已知点A(-4,2)、B(-1,-2),平行四边形ABCD的对角线交于坐标原点O.
如图,已知点A(-4,2)、B(-1,-2),平行四边形ABCD的对角线交于坐标原点O.(1)点A到x轴的距离是2.点B到y轴的距离是1.
(2)请直接写出点C、D的坐标:C(4,-2),D(1,2);
(3)观察图形,写出由点A到点C的变换过程:绕点O旋转180°.
(4)直接写出平行四边形ABCD的面积是20.
分析 (1)由点的坐标即可得出答案;
(2)利用中心对称图形的性质得出C,D两点坐标;
(3)利用平行四边形的性质以及结合平移的性质得出即可;
(4)利用SABCD的可以转化为边长为;5和4的矩形面积,进而求出即可.
解答 解:(1)点A到x轴的距离是2.点B到y轴的距离是1;
故答案为:2,1;
(2)∵四边形ABCD是平行四边形,
∴四边形ABCD关于O中心对称,
∵A(-4,2),B(-1,-2),
∴C(4,-2),D(1,2);
故答案为:4,-2;1,2;
(3)线段AB到线段CD的变换过程是:绕点O旋转180°;
故答案为:绕点O旋转180°;
(4)由(1)得:A到y轴距离为:4,D到y轴距离为:1,
A到x轴距离为:2,B到x轴距离为:2,
∴SABCD的可以转化为边长为;5和4的矩形面积,
∴SABCD=5×4=20;
故答案为:20.
点评 此题主要考查了平行四边形的性质以及中心对称图形的性质,根据题意得出SABCD的可以转化为矩形面积是解题关键.

练习册系列答案
 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目
18.点A(-2,-1)所在象限是( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
15. 小东、小林两名射箭运动员在赛前的某次测试中各射箭10次,成绩及各统计量如图、表所示:
小东、小林两名射箭运动员在赛前的某次测试中各射箭10次,成绩及各统计量如图、表所示:
若让你选择其中一名参加比赛则你选择的运动员是:小东,理由是:在水平相当的基础上小东的方差小说明波动小,发挥比小林稳定..
 小东、小林两名射箭运动员在赛前的某次测试中各射箭10次,成绩及各统计量如图、表所示:
小东、小林两名射箭运动员在赛前的某次测试中各射箭10次,成绩及各统计量如图、表所示:| 平均数 | 众数 | 中位数 | 方差 | |
| 小东 | 7.5 | 8 | 7.5 | 14.5 |
| 小林 | 7.5 | 9 | 7.5 | 34.5 |
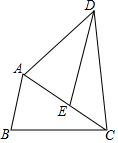 如图,在△ABC中,点E是AC上一点,AE=AB,过点E作DE∥AB,且DE=AC.
如图,在△ABC中,点E是AC上一点,AE=AB,过点E作DE∥AB,且DE=AC.