题目内容
16．解不等式组$\left\{\begin{array}{l}{\frac{2x-1}{3}-\frac{5x+1}{2}＜1}\\{5x-1＜3（x+1）}\end{array}\right.$并把解集在数轴上表示出来，并写出不等式组的所有非负整数解．分析 分别求出每一个不等式的解集，在数轴上表示出每个不等式的解集即可确定不等式组的解集，继而可得知不等式组的非负整数解．
解答 解：解不等式$\frac{2x-1}{3}$-$\frac{5x+1}{2}$＜1，得：x＞-1，
解不等式5x-1＜3（x+1），得：x＜2，
将不等式的解集表示在数轴上如下所示：
∴不等式组的解集为：-1＜x＜2，
则该不等式组的非负整数解有0、1．
点评 本题主要考查解一元一次不等式组的基本技能，准确求出每个不等式的解集是解题的根本，将不等式解集表示在数轴上从而确定不等式组得解集及其非负整数解是关键．
练习册系列答案
巧学巧练系列答案
相关题目
6．二元一次方程组的是（ ）
| A． | $\left\{\begin{array}{l}{x+y=3}\\{z+x=5}\end{array}\right.$ | B． | $\left\{\begin{array}{l}{x+y=5}\\{{y}^{2}=4}\end{array}\right.$ | ||
| C． | $\left\{\begin{array}{l}{x+y=3}\\{xy=2}\end{array}\right.$ | D． | $\left\{\begin{array}{l}{x=y+11}\\{{x}^{2}-2x=y+{x}^{2}}\end{array}\right.$ |
7．方程组$\left\{\begin{array}{l}{mx+2y=3}\\{x-3y=-4n}\end{array}\right.$有无数个解，则m、n的值为（ ）
| A． | m=$\frac{9}{8}$，n=-$\frac{2}{3}$ | B． | m=-$\frac{2}{3}$，n=$\frac{9}{8}$ | C． | m=$\frac{2}{3}$，n=-$\frac{9}{8}$ | D． | m=1，n=-$\frac{3}{4}$ |
4．如果不等式组$\left\{\begin{array}{l}{10-2x＞0}\\{x-m≥0}\end{array}\right.$有解，那么m的取值范围是（ ）
| A． | m＞5 | B． | m≥5 | C． | m＜5 | D． | m≤5 |
11．用配方法解下列方程，配方错误的是（ ）
| A． | x2+2x-99=0，化为（x+1）2=100 | B． | t2-7t-4=0，化为（t-$\frac{7}{2}$）2=$\frac{65}{4}$ | ||
| C． | x2+8x+9=0，化为（x+4）2=25 | D． | 3x2-4x-2=0，化为（x-$\frac{2}{3}$）2=$\frac{10}{9}$ |
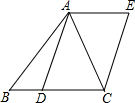如图，AD是△ABC的中线，四边形ADCE是平行四边形，设BC=a，AC=4，AB=$\sqrt{19}$，要使?ADCE是菱形，a的值是$\sqrt{35}$．
任意写一个一元一次不等式，它的不等号的左、右两边都要有两项，且它的解集如图所示，这个不等式可以写成2x+2＜x+1（答案不唯一）．