Question

1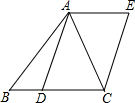．如图，AD是△ABC的中线，四边形ADCE是平行四边形，设BC=a，AC=4，AB=$\sqrt{19}$，要使?ADCE是菱形，a的值是$\sqrt{35}$．

Answer 1

分析 先连接DE交AC于O，根据?ADCE是菱形，得出AC⊥DE，再判断四边形ABDE是平行四边形，得出DE的长，最后根据菱形的性质，运用勾股定理求得CD的长，即可得出a的值．

解答 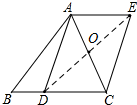解：连接DE交AC于O，则当?ADCE是菱形时，AC⊥DE，
∵AE∥BC，AE=CD，且AD是△ABC的中线，
∴AE∥BD，AE=BD，
∴四边形ABDE是平行四边形，
∴DE=AB=$\sqrt{19}$，
∴DO=$\frac{1}{2}$$\sqrt{19}$，
又∵AC=4，
∴CO=2，
∴Rt△COD中，CD=$\sqrt{（\frac{\sqrt{19}}{2}）^{2}+{2}^{2}}$=$\frac{\sqrt{35}}{2}$，
∴BC=2CD=$\sqrt{35}$，即a=$\sqrt{35}$．
故答案为：$\sqrt{35}$．

点评 本题主要考查了菱形的判定与性质，以及平行四边形的性质，解题时注意：菱形的对角线互相垂直，运用勾股定理可以求得线段的长．