题目内容
7.对实数a,b,定义运算“★”:a★b=$\left\{\begin{array}{l}{a(a≥0)}\\{b(a<0)}\end{array}\right.$,设y=(-x-1)★(x-1),则不等式y>0的解为( )| A. | x<1 | B. | -1<x<1 | C. | x>-1 | D. | x<-1或x>1 |
分析 根据题意得出关于x的不等式,求出x的取值范围即可.
解答 解:∵a★b=$\left\{\begin{array}{l}{a(a≥0)}\\{b(a<0)}\end{array}\right.$,设y=(-x-1)★(x-1),y>0,
∴-x-1>0或x-1>0,解得x<-1或x>1.
故选D.
点评 本题考查的是解一元一次不等式组,熟知不等式的基本性质是解答此题的关键.

练习册系列答案
相关题目
17.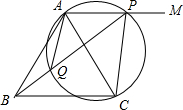 如图,等边△ABC边长为2,射线AM∥BC,P是射线AM上一动点(P不与A点重合),△APC的外接圆交BP于Q,则AQ长的最小值为( )
如图,等边△ABC边长为2,射线AM∥BC,P是射线AM上一动点(P不与A点重合),△APC的外接圆交BP于Q,则AQ长的最小值为( )
 如图,等边△ABC边长为2,射线AM∥BC,P是射线AM上一动点(P不与A点重合),△APC的外接圆交BP于Q,则AQ长的最小值为( )
如图,等边△ABC边长为2,射线AM∥BC,P是射线AM上一动点(P不与A点重合),△APC的外接圆交BP于Q,则AQ长的最小值为( )| A. | 1 | B. | $\sqrt{3}$ | C. | $\frac{{\sqrt{3}}}{3}$ | D. | $\frac{{2\sqrt{3}}}{3}$ |
2.中原宏发家具厂计划用甲种板材210m2,乙种板材250m2生产A、B两种款式的家具共50套,A、B两种款式的家具每套所需板材及获利情况如下表:
设生产A款家具x套,用这些板材生产的A、B两种款式的家具所获利润为y元.
(1)求y与x之间的函数关系式,并求出自变量x的取值范围;
(2)用这些板材生产A、B两种款式的家具时,如何安排可获利最大?
| 甲种板材(m2/套) | 乙种板材(m2/套) | 获利(元/套) | |
| A款 | 3 | 7 | 600 |
| B款 | 5 | 3 | 400 |
(1)求y与x之间的函数关系式,并求出自变量x的取值范围;
(2)用这些板材生产A、B两种款式的家具时,如何安排可获利最大?
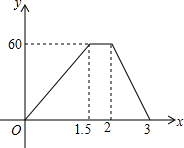 一辆汽车将一批货物从甲地运往乙地,到达乙地卸货后返回.设汽车从甲地出发x(h)时,汽车与甲地的距离为y(km),y与x的函数关系如图所示.根据图象信息解答下列问题.
一辆汽车将一批货物从甲地运往乙地,到达乙地卸货后返回.设汽车从甲地出发x(h)时,汽车与甲地的距离为y(km),y与x的函数关系如图所示.根据图象信息解答下列问题.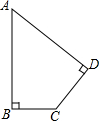 如图,已知一块四边形草地ABCD,其中∠A=45°,∠B=∠D=90°,AB=20m,CD=10m,求这块草地的面积.
如图,已知一块四边形草地ABCD,其中∠A=45°,∠B=∠D=90°,AB=20m,CD=10m,求这块草地的面积.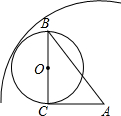 如图,Rt△ABC中,∠ACB=90°,BC=4cm,AC=3cm,⊙O是以BC为直径的圆,如果⊙O与⊙S相内切,那么⊙A的半径为$\sqrt{13}+2$cm.
如图,Rt△ABC中,∠ACB=90°,BC=4cm,AC=3cm,⊙O是以BC为直径的圆,如果⊙O与⊙S相内切,那么⊙A的半径为$\sqrt{13}+2$cm. 矩形ABCD四个内角平分线组成四边形MFNE,求证:四边形MFNE是正方形.
矩形ABCD四个内角平分线组成四边形MFNE,求证:四边形MFNE是正方形.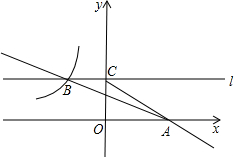 如图,在平面直角坐标系xOy中,直线y=-$\frac{1}{3}$+b与x轴交于点A,与双曲线y=-$\frac{6}{x}$在第二象限内交于点B(-3,a).
如图,在平面直角坐标系xOy中,直线y=-$\frac{1}{3}$+b与x轴交于点A,与双曲线y=-$\frac{6}{x}$在第二象限内交于点B(-3,a).