题目内容
12.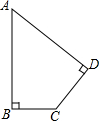 如图,已知一块四边形草地ABCD,其中∠A=45°,∠B=∠D=90°,AB=20m,CD=10m,求这块草地的面积.
如图,已知一块四边形草地ABCD,其中∠A=45°,∠B=∠D=90°,AB=20m,CD=10m,求这块草地的面积.
分析 分别延长AD,BC交于点E,所求四边形ABCD的面积=S△ABE-S△CED.由∠A=45°,∠B=∠D=90°,可得△ABE和△CDE都是等腰直角三角形,然后求出△ABE和△CDE的面积即可求解.
解答 解:分别延长AD,BC交于点E.如图所示,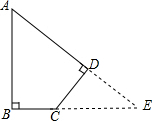
∵∠A=45°,∠B=∠D=90°,
∴∠DCE=∠DEB=∠A=45°,
∴AB=BE,CD=DE,
∵AB=20,CD=10,
∴BE=20,DE=10,
∵S△ABE=$\frac{1}{2}$AB•BE=200,S△CDE=$\frac{1}{2}$CD•DE=50,
∴四边形ABCD的面积=S△ABE-S△CDE=200-50=150m2.
即这块草地的面积为:150m2.
点评 本题考查了等腰直角三角形的性质,解题的关键是:通过作辅助线,构造新的直角三角形,利用四边形ABCD的面积=S△ABE-S△CED来求解.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
7.对实数a,b,定义运算“★”:a★b=$\left\{\begin{array}{l}{a(a≥0)}\\{b(a<0)}\end{array}\right.$,设y=(-x-1)★(x-1),则不等式y>0的解为( )
| A. | x<1 | B. | -1<x<1 | C. | x>-1 | D. | x<-1或x>1 |
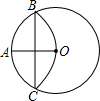 如图,⊙O的半径OA=6,以点A为圆心,OA为半径的弧交⊙O于B,C两点,求弦BC的长.
如图,⊙O的半径OA=6,以点A为圆心,OA为半径的弧交⊙O于B,C两点,求弦BC的长.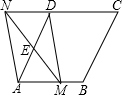 如图,在菱形ABCD中,AB=4,∠DAB=60°,点E是AD边的中点,点M是AB边上的一个动点(不与点A重合),延长ME交CD的延长线于点N,连接MD,AN.
如图,在菱形ABCD中,AB=4,∠DAB=60°,点E是AD边的中点,点M是AB边上的一个动点(不与点A重合),延长ME交CD的延长线于点N,连接MD,AN.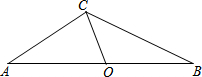 如图,已知钝角三角形ABC,∠A=35°,OC为边AB上的中线,将△AOC绕着点O顺时针旋转,点C落在BC边上的点C′处,点A落在点A′处,联结BA′,如果点A、C、A′在同一直线上,那么∠BA′C′的度数为20°.
如图,已知钝角三角形ABC,∠A=35°,OC为边AB上的中线,将△AOC绕着点O顺时针旋转,点C落在BC边上的点C′处,点A落在点A′处,联结BA′,如果点A、C、A′在同一直线上,那么∠BA′C′的度数为20°. 如图,在菱形ABCD中,AB=5,∠BCD=120°,则菱形的面积为$\frac{25\sqrt{3}}{2}$.
如图,在菱形ABCD中,AB=5,∠BCD=120°,则菱形的面积为$\frac{25\sqrt{3}}{2}$. 如图,在△ABC中,∠C=90°,AE,BE是△ABC的两个内角的平分线,AF,BF是△ABC的两个外角的平分线.求∠E,∠F的度数.
如图,在△ABC中,∠C=90°,AE,BE是△ABC的两个内角的平分线,AF,BF是△ABC的两个外角的平分线.求∠E,∠F的度数.