题目内容
10.已知关于x的一元二次方程x2-x+$\frac{1}{4}$m=0有两个实数根.(1)若m为正整数,求此方程的根;
(2)设此方程的一个实数根为b,若y=$\frac{1}{4}$m-2b2+2b+1,求y的取值范围.
分析 (1)表示出△,根据方程有两个实数根及m为正整数,可得m的值,继而可得方程的根.
(2)先得出m的取值范围,根据b是方程的一个实数根,可得2b2-2b+$\frac{1}{2}$m=0,整体代入,可得y的取值范围.
解答 解:(1)∵一元二次方程x2-x+$\frac{1}{4}$m=0有两个实数根,
∴△=1-m≥0,
∴m≤1,
又∵m为正整数,
∴m=1,
∴方程的根为$\frac{1}{2}$;
(2)∵△=1-m≥0,
∴m≤1,
∵b是方程的一个实数根,
∴b2-b+$\frac{1}{4}$m=0,
∴2b2-2b+$\frac{1}{2}$m=0,
∴y=$\frac{1}{4}$m-2b2+2b+1=$\frac{3}{4}$m+1,
即y的取值范围是:y≤$\frac{7}{4}$.
点评 本题考查了根的判别式及一元二次方程的解,解答本题的关键是掌握一元二次方程判别式与方程根的关系.

练习册系列答案
相关题目
1.科研人员在测试一枚火箭竖直向上升空时发现,火箭的高度h(m)与时间t(s)的关系数据如下:
(1)根据上表,以时间t为横轴,高度h为纵轴建立直角坐标系,并描出上述各点;
(2)你能根据坐标系中各点的变化趋势确定h关于t的函数类型吗?
(3)请由以上数据确定h与t的函数表达式;
(4)你能由上述三种函数的表示方式求出该火箭的最高射程是多少吗?你是根据哪种表示方式求解的?
| 时间t/s | 1 | 5 | 10 | 15 | 20 | 25 |
| 火箭高度h/m | 155 | 635 | 1010 | 1135 | 1010 | 635 |
(2)你能根据坐标系中各点的变化趋势确定h关于t的函数类型吗?
(3)请由以上数据确定h与t的函数表达式;
(4)你能由上述三种函数的表示方式求出该火箭的最高射程是多少吗?你是根据哪种表示方式求解的?
 如图,平面直角坐标系中,已知△ABC中,A(1,3),B(2,2),C(6,5),求△ABC的面积.
如图,平面直角坐标系中,已知△ABC中,A(1,3),B(2,2),C(6,5),求△ABC的面积.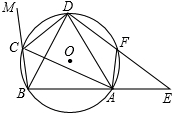 如图,△ABC内接于圆,∠BCA外角的平分线CD交该圆于点D,F为弧AD上一点,连接并延长DF与BA的延长线交于点E.连结BD,AF.
如图,△ABC内接于圆,∠BCA外角的平分线CD交该圆于点D,F为弧AD上一点,连接并延长DF与BA的延长线交于点E.连结BD,AF.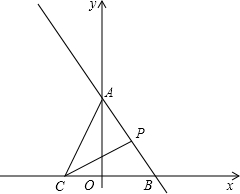 如图,在平面直角坐标系中,直线l:y=-$\frac{4}{3}$x+4与y轴、x轴分别交于点A、B,若点C是x轴负半轴上一点,当AB=BC时,若点P是l上一动点,点N在坐标轴上,当以A,C,P,N为顶点的四边形是平行四边形时,求点P,N的坐标.
如图,在平面直角坐标系中,直线l:y=-$\frac{4}{3}$x+4与y轴、x轴分别交于点A、B,若点C是x轴负半轴上一点,当AB=BC时,若点P是l上一动点,点N在坐标轴上,当以A,C,P,N为顶点的四边形是平行四边形时,求点P,N的坐标.