题目内容
4. 如图,矩形ABCD位于二次函数y=-2x2+4x与x轴所围区域内,BC边在x轴上,A,D两点位于二次函数图象上,则矩形ABCD周长的最大值为( )
如图,矩形ABCD位于二次函数y=-2x2+4x与x轴所围区域内,BC边在x轴上,A,D两点位于二次函数图象上,则矩形ABCD周长的最大值为( )| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
分析 首先求出M的坐标(2,0),设A(m,-2m2+4m),根据对称性得BC=2-2m,构建二次函数,利用二次函数的性质即可解决问题.
解答 解:∵y=-2x2+4x,
∴当y=0时,x=0或2,
∴M(2,0),设A(m,-2m2+4m),
则AB=-2m2+4m,
根据对称性OB=CM=m,
∴BC=2-2m,
∴矩形ABCD的周长L为=2(-2m2+4m+2-2m)=-4(m-$\frac{1}{2}$)2+5,
∵-4<0,
∴当m=$\frac{1}{2}$时,L有最大值.L的最大值为5.
故选D.
点评 本题考查抛物线与x轴的交点、矩形的性质等知识,解题的关键是学会构建二次函数,通过配方法确定周长的最大值,

练习册系列答案
 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案
相关题目
19.在式子$\frac{1}{x-1}$,$\frac{1}{x-2}$,$\sqrt{x-1}$,$\sqrt{x-2}$中,x可以取1和2的是( )
| A. | $\frac{1}{x-1}$ | B. | $\frac{1}{x-2}$ | C. | $\sqrt{x-1}$ | D. | $\sqrt{x-2}$ |
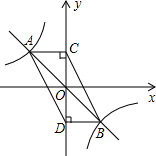 如图,函数y=-x与函数y=-$\frac{4}{x}$的图象相交于A、B两点,过A、B两点分别作y轴的垂线,垂足分别为点C、D,则四边形ACBD的面积为( )
如图,函数y=-x与函数y=-$\frac{4}{x}$的图象相交于A、B两点,过A、B两点分别作y轴的垂线,垂足分别为点C、D,则四边形ACBD的面积为( )