题目内容
11．解不等式组$\left\{\begin{array}{l}2x+4＜5（x+2）\\ \frac{2x}{3}+1≥x\end{array}$并把它的解集在数轴上表示出来．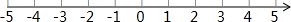
分析 分别解两个不等式得到x＞-2和x≤3，再利用数轴表示解集，然后根据大小小大中间找确定不等式组的解集．
解答 解：$\left\{\begin{array}{l}{2x+4＜5（x+2）①}\\{\frac{2x}{3}+1≥x②}\end{array}\right.$
解不等式①得x＞-2，
解不等式②得x≤3，
数轴表示解集为：
所以不等式组的解集是-2＜x≤3．
点评 本题考查了一元一次不等式组：解一元一次不等式组时，一般先求出其中各不等式的解集，再求出这些解集的公共部分，利用数轴可以直观地表示不等式组的解集．解集的规律：同大取大；同小取小；大小小大中间找；大大小小找不到．
练习册系列答案
智慧小复习系列答案
相关题目
1．点P（x，y）在第二象限内，且|x|=2，|y|=3，则点P关于y轴的对称点的坐标为（ ）
| A． | （2，3） | B． | （-2，-3） | C． | （3，-2） | D． | （-3，2） |
若关于m的不等式的解集如图所示，则关于x的不式（m-3）x＜3-m的解集为x＞-1．
如图，已知∠1=∠2，∠A=∠3，能否判断AB∥CD？说明你的理由．