题目内容
1.先化简,再求值:$\frac{2}{x+1}$+$\frac{3}{x-1}$+$\frac{4}{{x}^{2}-1}$,其中x=$\sqrt{6}$.分析 先通分,再把分子相加减,最后把x的值代入进行计算即可.
解答 解:原式=$\frac{2(x-1)}{(x+1)(x-1)}$+$\frac{3(x+1)}{(x+1)(x-1)}$+$\frac{4}{(x+1)(x-1)}$
=$\frac{2x-2+3x+3+4}{(x+1)(x-1)}$
=$\frac{5(x+1)}{(x+1)(x-1)}$
=$\frac{5}{x-1}$,
当x=$\sqrt{6}$时,原式=$\frac{5}{\sqrt{6}-1}$=$\sqrt{6}$+1.
点评 本题考查的是分式的化简求值,熟知异分母的分式相加减的法则是解答此题的关键.

练习册系列答案
 精英口算卡系列答案
精英口算卡系列答案 应用题点拨系列答案
应用题点拨系列答案
相关题目
9.下表是某校合唱团成员的年龄分布
对于不同的x,下列关于年龄的统计量不会发生改变的是( )
| 年龄/岁 | 13 | 14 | 15 | 16 |
| 频数 | 5 | 15 | x | 10-x |
| A. | 平均数、中位数 | B. | 众数、中位数 | C. | 平均数、方差 | D. | 中位数、方差 |
10. 如图是一个由5张纸片拼成的平行四边形,相邻纸片之间互不重叠也无缝隙,其中两张等腰直角三角形纸片的面积都为S1,另两张直角三角形纸片的面积都为S2,中间一张正方形纸片的面积为S3,则这个平行四边形的面积一定可以表示为( )
如图是一个由5张纸片拼成的平行四边形,相邻纸片之间互不重叠也无缝隙,其中两张等腰直角三角形纸片的面积都为S1,另两张直角三角形纸片的面积都为S2,中间一张正方形纸片的面积为S3,则这个平行四边形的面积一定可以表示为( )
 如图是一个由5张纸片拼成的平行四边形,相邻纸片之间互不重叠也无缝隙,其中两张等腰直角三角形纸片的面积都为S1,另两张直角三角形纸片的面积都为S2,中间一张正方形纸片的面积为S3,则这个平行四边形的面积一定可以表示为( )
如图是一个由5张纸片拼成的平行四边形,相邻纸片之间互不重叠也无缝隙,其中两张等腰直角三角形纸片的面积都为S1,另两张直角三角形纸片的面积都为S2,中间一张正方形纸片的面积为S3,则这个平行四边形的面积一定可以表示为( )| A. | 4S1 | B. | 4S2 | C. | 4S2+S3 | D. | 3S1+4S3 |
11.化简$\frac{{a}^{2}-{b}^{2}}{ab}$-$\frac{ab-{b}^{2}}{ab-{a}^{2}}$等于( )
| A. | $\frac{b}{a}$ | B. | $\frac{a}{b}$ | C. | -$\frac{b}{a}$ | D. | -$\frac{a}{b}$ |
 由一些相同的小正方体搭成的几何体的左视图和俯视图如图所示,请在网格中涂出一种该几何体的主视图,且使该主视图是轴对称图形.
由一些相同的小正方体搭成的几何体的左视图和俯视图如图所示,请在网格中涂出一种该几何体的主视图,且使该主视图是轴对称图形. 福州市2011-2015年常住人口数统计如图所示.
福州市2011-2015年常住人口数统计如图所示. 从一个边长为3cm的大立方体挖去一个边长为1cm的小立方体,得到的几何体如图所示,则该几何体的左视图正确的是( )
从一个边长为3cm的大立方体挖去一个边长为1cm的小立方体,得到的几何体如图所示,则该几何体的左视图正确的是( )



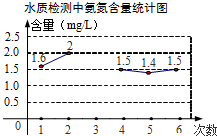 为监测某河道水质,进行了6次水质检测,绘制了如图的氨氮含量的折线统计图.若这6次水质检测氨氮含量平均数为1.5mg/L,则第3次检测得到的氨氮含量是1mg/L.
为监测某河道水质,进行了6次水质检测,绘制了如图的氨氮含量的折线统计图.若这6次水质检测氨氮含量平均数为1.5mg/L,则第3次检测得到的氨氮含量是1mg/L.