题目内容
身高1.7m的人站在两棵树之间，距较高的树5m，距较矮的树3m，若此人观察两棵树所成的视线的夹角为90°，且较矮的树的高为4m，求较高的树的高．
考点：相似三角形的应用
专题：
分析：根据题意作出图形，利用相似三角形的知识求解；
解答：
解：根据题意得：AB=4，EC=BD=3，CH=DF=5，CD=1.7，∠ACE=90°，
∴AG=2.3，
∴∠ACG+∠ECH=90°，
∵∠A+∠ACG=90°
∴∠A=∠ECH，
∴△AGC∽△CHE
∴
=
即：
=
∴HE≈6.5m，
∴EF=EH+HF=6.5+1.7=8.2米．
解：根据题意得：AB=4，EC=BD=3，CH=DF=5，CD=1.7，∠ACE=90°，∴AG=2.3，
∴∠ACG+∠ECH=90°，
∵∠A+∠ACG=90°
∴∠A=∠ECH，
∴△AGC∽△CHE
∴
| AG |
| CH |
| GC |
| HE |
即：
| 2.3 |
| 5 |
| 3 |
| HE |
∴HE≈6.5m，
∴EF=EH+HF=6.5+1.7=8.2米．
点评：本题考查了相似三角形的应用，解题的关键是根据题意作出图形，将实际问题抽象为数学问题解决．
练习册系列答案
期末集结号系列答案
相关题目
一个正方形的边长增加2cm，它的面积就增加了24cm2，这个正方形原来的边长是（ ）
| A、5cm | B、6cm |
| C、8cm | D、10cm |
点P在直线y=-x+4上，并且它的纵坐标是3，那么点P关于x轴的对称点P′的坐标为（ ）
| A、（1，3） |
| B、（1，-3） |
| C、（-1，3） |
| D、（-1，-3） |
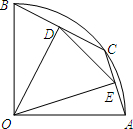如图，在半径为2的扇形AOB中，∠AOB=90°，点C是弧AB上的一个动点（不与点A、B重合），OD⊥BC，OE⊥AC，垂足分别为D、E，则线段DE的长为（ ）若⊙O1、⊙O2的直径分别为4和6，圆心距O1O2=2，则⊙O1与⊙O2的位置关系是（ ）
| A、相交 | B、外离 | C、外切 | D、内切 |
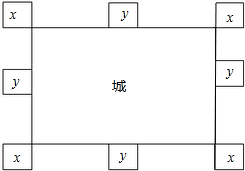戚继光是古代著名的抗倭将领，有一次，当倭寇来袭时，戚家军主力尚未到达，城里的兵力仅360人，戚继光思考着怎样布置兵力，使敌人不论从哪一方向察看，都有100名士兵在把手，经过思考，戚继光决定抽调100人去绕道袭击敌人的粮草．有人担心城内兵力太少，戚继光却说：“没关系，我会重新布置，这260人在布置好后，敌人无论从哪一面察看，反而会认为士兵增加了25名．”随后他画了一张图让大家看（如图）
如图，在☉O中，AB是直径，C、D是圆上两点，使得AD=BC．求证：AC=BD．