题目内容
9.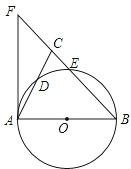 如图,在△ABC中,BA=BC,以AB为直径的⊙O分别交AC、BC于点D、E,BC的延长线与⊙O的切线AF交于点F.
如图,在△ABC中,BA=BC,以AB为直径的⊙O分别交AC、BC于点D、E,BC的延长线与⊙O的切线AF交于点F.(1)求证:∠ABC=2∠CAF;
(2)若AC=$\frac{{\sqrt{10}}}{2}$,EB=2,求圆心O到BE的距离.
分析 (1)首先连接BD,由AB为直径,可得∠ADB=90°,又由AF是⊙O的切线,易证得∠CAF=∠ABD.然后由BA=BC,证得:∠ABC=2∠CAF;
(2)连接AE,过点O作OH⊥BE,设CE=x,易证OH是三角形ABE的中位线,所以求出AE的长,则OH的长可求出,即圆心O到BE的距离可求出.
解答 (1)证明:如图1所示,连接BD.
∵AB为⊙O的直径,
∴∠ADB=90°,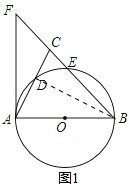
∴∠DAB+∠ABD=90°.
∵AF是⊙O的切线,
∴∠FAB=90°,
即∠DAB+∠CAF=90°.
∴∠CAF=∠ABD.
∵BA=BC,∠ADB=90°,
∴∠ABC=2∠ABD.
∴∠ABC=2∠CAF;
(2)连接AE,过点O作OH⊥BE,如图2所示
∵AB是⊙O的直径,
∴AE⊥BE,
∵AO=BO,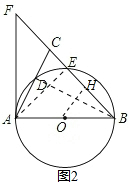
∴BH=EH,
∴OH是△AEB的中位线,
∵AB是⊙O的直径,
∴BD⊥AC,
∵AB=BC,
∴AD=$\frac{1}{2}$AC=$\frac{\sqrt{10}}{4}$,
设CE=x,则BC=BE+CE=x+2,
∴AB=x+2,
∴AE2=AC2-CE2=$\frac{10}{4}$-x2,
∴AB2=AE2+BE2=$\frac{10}{4}$-x2+4,
即(x+2)2=$\frac{10}{4}$-x2+4,
解得:x=0.5或-2.5(舍),
∴AE=$\frac{9}{4}$,
∴OH=$\frac{1}{2}$AE=$\frac{9}{8}$.
点评 本题主要考查了切线的性质、三角函数以及勾股定理,注意掌握辅助线的作法,注意掌握数形结合思想与方程思想的应用是解答此题的关键.

练习册系列答案
 阶梯计算系列答案
阶梯计算系列答案
相关题目
19.下列各式计算结果为a7的是( )
| A. | (-a)2•(-a)5 | B. | (-a)2•(-a5) | C. | (-a2)•(-a)5 | D. | (-a)•(-a)6 |
17.准备两组相同的牌,每组两张且大小相同,两张牌的牌面数字分别是0,1,从每组牌中各摸出一张牌,两张牌的牌面数字和为1的概率为( )
| A. | $\frac{3}{4}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{1}{4}$ |
4.在下列各式①$\frac{1}{2}$(1-x);②$\frac{2x}{π-3}$;③$\frac{{x}^{2}-{y}^{2}}{2}$;④$\frac{3}{x+y}$;⑤$\frac{5{y}^{2}}{x}$中,是分式有( )
| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
19.下列各组数据分别是三角形的三边长,其中能构成直角三角形的是( )
| A. | 2cm、4cm、5cm | B. | 1cm、1cm、$\sqrt{2}$cm | C. | 1cm、2cm、2cm | D. | $\sqrt{3}$cm、2cm、$\sqrt{5}$cm |