题目内容
18.在实数范围内分解因式:2x4y-18y=2y(x2+3)(x+$\sqrt{3}$)(x-$\sqrt{3}$).分析 先提公因式2y,再根据平方差公式分解即可得出答案.
解答 解:2x4y-18y=2y(x4-9)
=2y(x2+3)(x2-3)
=2y(x2+3)(x+$\sqrt{3}$)(x-$\sqrt{3}$),
故答案为:2y(x2+3)(x+$\sqrt{3}$)(x-$\sqrt{3}$).
点评 本题考查了分解因式(提公因式法和用平方差公式分解因式法),熟悉分解因式的一般步骤是基本,对公式的掌握是关键.

练习册系列答案
相关题目
6.下列说法中错误的是( )
| A. | 直径是圆中最长的弦 | |
| B. | 平分弦的直径垂直于弦,并且平分弦所对的两条弧 | |
| C. | 不在同一直线上的三点确定一个圆 | |
| D. | 在同圆或等圆中,能重合的两弧叫做等弧 |
8.函数$y=\frac{x}{x+3}$中,自变量x的取值范围是( )
| A. | x>-3 | B. | x<-3 | C. | x≠-3 | D. | x≠3 |
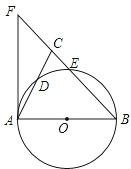 如图,在△ABC中,BA=BC,以AB为直径的⊙O分别交AC、BC于点D、E,BC的延长线与⊙O的切线AF交于点F.
如图,在△ABC中,BA=BC,以AB为直径的⊙O分别交AC、BC于点D、E,BC的延长线与⊙O的切线AF交于点F.