题目内容
1.已知:am=2,an=5,则a3m+n=40.分析 首先根据幂的乘方的运算方法,可得a3m=(am)3=8,然后根据同底数幂的乘法法则,求出算式a3m+n的值是多少即可.
解答 解:∵am=2,
∴a3m=(am)3=23=8,
∴a3m+n=a3m•an
=8×5
=40
故答案为:40.
点评 (1)此题主要考查了幂的乘方和积的乘方,要熟练掌握,解答此题的关键是要明确:①(am)n=amn(m,n是正整数);②(ab)n=anbn(n是正整数).
(2)此题还考查了同底数幂的乘法法则:同底数幂相乘,底数不变,指数相加,要熟练掌握,解答此题的关键是要明确:①底数必须相同;②按照运算性质,只有相乘时才是底数不变,指数相加.

练习册系列答案
 步步高达标卷系列答案
步步高达标卷系列答案
相关题目
6.下列说法中错误的是( )
| A. | 直径是圆中最长的弦 | |
| B. | 平分弦的直径垂直于弦,并且平分弦所对的两条弧 | |
| C. | 不在同一直线上的三点确定一个圆 | |
| D. | 在同圆或等圆中,能重合的两弧叫做等弧 |
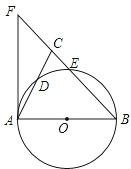 如图,在△ABC中,BA=BC,以AB为直径的⊙O分别交AC、BC于点D、E,BC的延长线与⊙O的切线AF交于点F.
如图,在△ABC中,BA=BC,以AB为直径的⊙O分别交AC、BC于点D、E,BC的延长线与⊙O的切线AF交于点F.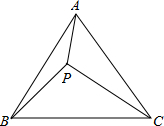 已知,如图,P为等边三角形ABC内一点,PA=3,PB=4,PC=5,求△ABC的面积.
已知,如图,P为等边三角形ABC内一点,PA=3,PB=4,PC=5,求△ABC的面积.