题目内容
18．
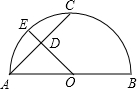如图，AB为半圆直径，O为圆心，C为半圆上一点，E是弧AC上的一点，且OE⊥AC交弦AC于点D．若AC=8cm，DE=2cm，求OD的长．
分析 设OD=x，则OA=2+x，根据勾股定理列方程可得结果．
解答 解：设OD=x，则OA=2+x，
∵OD⊥AC，
∴AD=$\frac{1}{2}$AC=4，
∠ADO=90°，
由勾股定理得：42+x2=（2+x）2，
解得：x=3，
∴OD的长为3cm．
点评 此题考查了圆中求半径的问题，此类在圆中涉及弦长、半径、圆心角的计算的问题，常把半弦长，半圆心角，圆心到弦距离转换到同一直角三角形中，然后通过直角三角形勾股定理予以求解．
练习册系列答案
阅读快车系列答案
相关题目
如图，图形我们把它称为“8字形”，请说明∠A+∠B=∠C+∠D．
6．已知抛物线y=ax2+bx+c（b＞a＞0）与x轴最多有一个交点，现有以下四个结论：①该抛物线的对称轴在y轴左侧；②关于x的方程ax2+bx+c=0无实数根；③a-b+c≥0；④$\frac{a+b+c}{b-a}$的最小值为3，其中正确结论的个数是（ ）
| A． | 1个 | B． | 2个 | C． | 3个 | D． | 4个 |
3．下列各组数中互为相反数的是（ ）
| A． | -2与$\sqrt{{{（-2）}^2}}$ | B． | -2与$\root{3}{-8}$ | C． | -2与$-\frac{1}{2}$ | D． | 2与|-2| |