题目内容
17.求直线y=4-3x和直线y=2x-1与y轴围成的三角形面积.分析 联立方程组求得两直线的交点,令x=0求得相应的y的值即可求得直线与y轴的交点坐标,然后利用三角形的面积公式进行计算.
解答 解:依题意得,$\left\{\begin{array}{l}{y=4-3x}\\{y=2x-1}\end{array}\right.$,
解得 $\left\{\begin{array}{l}{x=1}\\{y=1}\end{array}\right.$,
则两直线的交点(1,1).
由y=4-3x知直线y=4-3x与y轴的交点为(0,4),
由y=2x-1知直线y=2x-1与y轴的交点为 (0,1).
所以 S=$\frac{1}{2}$×3×1=$\frac{3}{2}$.
点评 此题考查的是一次函数图象上点的坐标特点,即一次函数y=kx+b与x轴的交点为(-$\frac{b}{k}$,0),与y轴的交点为(0,b).

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
7.下列命题中,是真命题的是( )
| A. | 三个点确定一个圆 | |
| B. | 同弧所对的圆周角与圆心角相等 | |
| C. | 直径是圆中最长的弦 | |
| D. | 圆是轴对称图形,不是中心对称图形 |
5.若(a+$\sqrt{2}$)2与|b-1|互为相反数,则2b-a的值为( )
| A. | 2$\sqrt{2}$ | B. | $\sqrt{2}$+2 | C. | $\sqrt{2}$-2 | D. | 2-$\sqrt{2}$ |
 如图,点A的坐标是(2,1),点B的坐标是(5,1),过点A的直线l的表达式为y=2x+b,点C在直线l上运动,在直线OA上是否存在一点D,使得以A,B,C,D为顶点的四边形是平行四边形?若存在,求出点D的坐标;若不存在,请说明理由.
如图,点A的坐标是(2,1),点B的坐标是(5,1),过点A的直线l的表达式为y=2x+b,点C在直线l上运动,在直线OA上是否存在一点D,使得以A,B,C,D为顶点的四边形是平行四边形?若存在,求出点D的坐标;若不存在,请说明理由.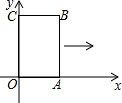 如图,矩形OABC的两条边在坐标轴上,OA=1,OC=2,现将此矩形向右平移1个单位,若平移得到的矩形的边与反比例函数图象有两个交点,它们的纵坐标之差的绝对值为0.6,求该反比例函数解析式.
如图,矩形OABC的两条边在坐标轴上,OA=1,OC=2,现将此矩形向右平移1个单位,若平移得到的矩形的边与反比例函数图象有两个交点,它们的纵坐标之差的绝对值为0.6,求该反比例函数解析式.