题目内容
 如图,已知AO⊥OC,OB⊥OD,∠AOB=142°,求∠COD的度数.
如图,已知AO⊥OC,OB⊥OD,∠AOB=142°,求∠COD的度数.考点:垂线
专题:
分析:首先根据垂直定义可得∠AOC=∠DOB=90°,再由∠AOB=142°可计算出∠BOC的度数,然后再利用90°-∠BOC即可得到∠COD的度数.
解答:解:∵AO⊥OC,OB⊥OD,
∴∠AOC=∠DOB=90°,
∵∠AOB=142°,
∴∠BOC=142°-90°=52°,
∴∠COD=90°-52°=38°.
∴∠AOC=∠DOB=90°,
∵∠AOB=142°,
∴∠BOC=142°-90°=52°,
∴∠COD=90°-52°=38°.
点评:此题主要考查了垂直的定义,角的和差,要注意领会由垂直得直角这一要点,求出∠BOC的度数是解题的关键.

练习册系列答案
 华东师大版一课一练系列答案
华东师大版一课一练系列答案
相关题目
 如图,双曲线y=
如图,双曲线y=| 2 |
| x |
A、
| ||
| B、6 | ||
| C、3 | ||
D、
|
 如图所示的几何体的俯视图是( )
如图所示的几何体的俯视图是( )A、 |
B、 |
C、 |
D、 |
若n边形的内角和比外角和大180°,则n的值为( )
| A、5 | B、6 | C、7 | D、8 |
已知a、b、c是统一平面内的三条直线,则下列命题中,属于假命题的是( )
| A、如果a∥b,b⊥c,那么a⊥c |
| B、如果a∥b,b∥c,那么a∥c |
| C、如果a⊥b,b⊥c,那么a⊥c |
| D、如果a⊥b,b⊥c,那么a∥c |
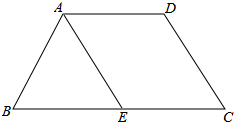 如图,等腰梯形ABCD中,AD∥BC,AE∥DC,∠AEB=60°,AB=AD=2cm,则梯形ABCD的周长为( )
如图,等腰梯形ABCD中,AD∥BC,AE∥DC,∠AEB=60°,AB=AD=2cm,则梯形ABCD的周长为( )| A、12cm | B、10cm |
| C、8cm | D、6cm |
 如图所示,已知等边三角形ABC的两个顶点坐标为A(-4,0),B(2,0),CH⊥AB,试求点C的坐标和△ABC的面积.
如图所示,已知等边三角形ABC的两个顶点坐标为A(-4,0),B(2,0),CH⊥AB,试求点C的坐标和△ABC的面积.
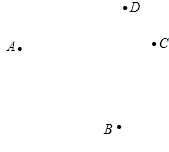 已知平面上A、B、C、D四个点,按下列要求画出图形:
已知平面上A、B、C、D四个点,按下列要求画出图形: