题目内容
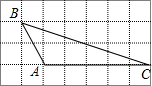 如图,在4×7的正方形网格中,有一个格点三角形ABC,那么∠ABC的正弦值是( )
如图,在4×7的正方形网格中,有一个格点三角形ABC,那么∠ABC的正弦值是( )A、
| ||||||
B、
| ||||||
C、
| ||||||
D、
|
考点:勾股定理,锐角三角函数的定义
专题:网格型
分析:先根据勾股定理求出BC及AB的长,作AK⊥BC,垂足为K,根据三角形的面积公式求出AK的长,根据锐角三角函数的定义即可得出结论.
解答: 解:由勾股定理得,BC=
解:由勾股定理得,BC=
=2
,AB=
=
,
作AK⊥BC,垂足为K.
∵
BC•AK=
AC•2,
即
×2
•AK=
×5×2,
∴AK=
=
=
,
∴sin∠ABC=
=
.
故选D.
 解:由勾股定理得,BC=
解:由勾股定理得,BC=| 62+22 |
| 10 |
| 22+12 |
| 5 |
作AK⊥BC,垂足为K.
∵
| 1 |
| 2 |
| 1 |
| 2 |
即
| 1 |
| 2 |
| 10 |
| 1 |
| 2 |
∴AK=
| 5 | ||
|
5
| ||
| 10 |
| ||
| 2 |
∴sin∠ABC=
| ||||
|
| ||
| 2 |
故选D.
点评:本题考查的是勾股定理,熟知在任何一个直角三角形中,两条直角边长的平方之和一定等于斜边长的平方是解答此题的关键.

练习册系列答案
相关题目
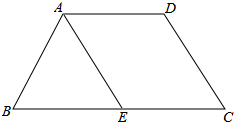 如图,等腰梯形ABCD中,AD∥BC,AE∥DC,∠AEB=60°,AB=AD=2cm,则梯形ABCD的周长为( )
如图,等腰梯形ABCD中,AD∥BC,AE∥DC,∠AEB=60°,AB=AD=2cm,则梯形ABCD的周长为( )| A、12cm | B、10cm |
| C、8cm | D、6cm |
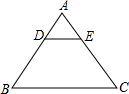 如图,△ABC是等腰三角形,顶点为A、D、E分别在腰AB、AC上,连接DE,若△ADE是等腰三角形,且顶点为A,则下列结论中错误的是( )
如图,△ABC是等腰三角形,顶点为A、D、E分别在腰AB、AC上,连接DE,若△ADE是等腰三角形,且顶点为A,则下列结论中错误的是( )| A、AD=AE |
| B、BD=CE |
| C、DE∥BC |
| D、△ADE≌△ABC |
| 1 |
| 2 |
| 3 |
| 2015 |
| 5 |
| A、18个 | B、19个 |
| C、20个 | D、21个 |
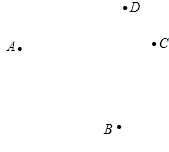 已知平面上A、B、C、D四个点,按下列要求画出图形:
已知平面上A、B、C、D四个点,按下列要求画出图形: 如图,AB为⊙O的直径,AD平分∠BAC交⊙O于点D,DE⊥AC交AC的延长线于点E,FB是⊙O的切线交AD的延长线于点F.
如图,AB为⊙O的直径,AD平分∠BAC交⊙O于点D,DE⊥AC交AC的延长线于点E,FB是⊙O的切线交AD的延长线于点F. 如图,在?ABCD中,E,F分别为边AB、CD的中点,BD是对角线,过A作AG∥DB交CB的延长线于点G.
如图,在?ABCD中,E,F分别为边AB、CD的中点,BD是对角线,过A作AG∥DB交CB的延长线于点G.