��Ŀ����
��ʮ�������һ����Ϸ��ʹ����������Ŀ�������ͬ��������������Ŀ����Ա���������Ŀ�����С��
 ����4��������4��������2��.
���������������������Ҫ��ʹ����������Ŀ�������ͬ����������Ŀ����Ա���������Ŀ�����С��ֻҪ�����������ͬ������ĸ������ڻ���ĸ������ɣ�
���������������֪��10�����������+�������+���������10
����������Ŀ�������ͬ
��������=�������=1��2��3��4
��������������������������������:1��1��8��2��...
����4��������4��������2��.
���������������������Ҫ��ʹ����������Ŀ�������ͬ����������Ŀ����Ա���������Ŀ�����С��ֻҪ�����������ͬ������ĸ������ڻ���ĸ������ɣ�
���������������֪��10�����������+�������+���������10
����������Ŀ�������ͬ
��������=�������=1��2��3��4
��������������������������������:1��1��8��2��...
 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д���ͼ����?ABCD�У�AB��AD�������²�����ͼ���Ե�AΪԲ�ģ�С��AD�ij�Ϊ�뾶�������ֱ�AB��AD�ڵ�E��F���ٷֱ��Ե�E��FΪԲ�ģ�����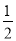 EF�ij�Ϊ�뾶�������������ڵ�G��������AG��CD�ڵ�H�������н����в��������������ó����ǣ�������
EF�ij�Ϊ�뾶�������������ڵ�G��������AG��CD�ڵ�H�������н����в��������������ó����ǣ�������
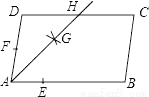
A. AGƽ�֡�DAB B. AD=DH C. DH=BC D. CH=DH
 D
������������������ɽ�ƽ���ߵ��������������֪AGƽ�֡�DAB��A��ȷ����DAH����BAH����AB��DC�����ԡ�BAH����ADH�����ԣ���DAH����ADH�����ԣ�AD��DH����AD��BC�����ԣ�DH��BC��B��C��ȷ���ʴ�ѡD.
D
������������������ɽ�ƽ���ߵ��������������֪AGƽ�֡�DAB��A��ȷ����DAH����BAH����AB��DC�����ԡ�BAH����ADH�����ԣ���DAH����ADH�����ԣ�AD��DH����AD��BC�����ԣ�DH��BC��B��C��ȷ���ʴ�ѡD. ��������y=x2��4x+4��y������ƽ��9����λ����������������x�������ύ�ڵ�B����y�ύ�ڵ�C������ΪD����1����B��C��D���ꣻ��2����BCD�������
 ��1����5��0������2��15.
�����������������
��1������ͼ��ƽ�ƵĹ�����������ߵĽ���ʽ���䷽��ɵö���D�����꣬��y=0���ɵ�B�����꣬��x=0���ɵ�C�����ꣻ
��2����D��DA��y���ڵ�A������ͼ�ε�����ĺ�������BCD�����.
���������
��1��������y=x2��4x+4��y������ƽ��9����λ�����ʽ��y=x2��4x+4��9����y=x2��4x��5��
...
��1����5��0������2��15.
�����������������
��1������ͼ��ƽ�ƵĹ�����������ߵĽ���ʽ���䷽��ɵö���D�����꣬��y=0���ɵ�B�����꣬��x=0���ɵ�C�����ꣻ
��2����D��DA��y���ڵ�A������ͼ�ε�����ĺ�������BCD�����.
���������
��1��������y=x2��4x+4��y������ƽ��9����λ�����ʽ��y=x2��4x+4��9����y=x2��4x��5��
... ���꣬6��12��Ϊ����ڣ��ڶ����ǰϦ����λͬѧ��ij���е���һ�ֽ���Ϊ2Ԫ�����ӵ���������������С���ṩ����Ϣ�����С����С����������⣮
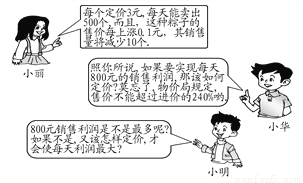
 (1)������Ϊ4Ԫʱ����ʵ��ÿ��800Ԫ����������(2)������Ϊ4.8Ԫʱ��ÿ��������������
�������������������1��С��������Ҫ��һԪ���η�������������Ĺؼ���Ū�壺��ʵ��ÿ��800Ԫ����Ķ���ΪxԪ/��ʱ��ÿһ�����ӵ�����Ϊ��x-2��Ԫ��һ��������500-��10�������ӣ����������з��̵ã���x-2)��500-��10��=800�����x1=4,x2=6����Ӧ����ʵ������ȷ������ֵ�Ƿ�...
(1)������Ϊ4Ԫʱ����ʵ��ÿ��800Ԫ����������(2)������Ϊ4.8Ԫʱ��ÿ��������������
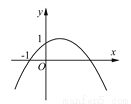
�������������������1��С��������Ҫ��һԪ���η�������������Ĺؼ���Ū�壺��ʵ��ÿ��800Ԫ����Ķ���ΪxԪ/��ʱ��ÿһ�����ӵ�����Ϊ��x-2��Ԫ��һ��������500-��10�������ӣ����������з��̵ã���x-2)��500-��10��=800�����x1=4,x2=6����Ӧ����ʵ������ȷ������ֵ�Ƿ�... ��ͼ�����κ���y��ax2��bx��c(a��0)��ͼ��Ķ����ڵ�һ���ޣ��ҹ���(0��1)��(��1��0)�����н��ۣ���ab��0����b2��4a����0��a��b��c��2����0��b��1���ݵ�x����1ʱ��y��0.������ȷ���۵ĸ�����( )
A. 5�� B. 4�� C. 3�� D. 2��
 B
���������������ߵĶԳ���x=-��y���Ҳ࣬�����ж�a��b��ţ��ɴ�ȷ������ȷ��
����������x������������õ�b2-4ac��0���������߹��㣨0��1�����ó�c=1���ɴ��ж�����ȷ��
��a-b+c=0����b��0�ó�a+b+c=2b��0����b��1��c=1��a��0���ó�a+b+c��a+1+1��2���ɴ��ж�����ȷ��
�������߹��㣨-1��0�����ó�a-b+c=0����a=b-1����a��0�ó�...
B
���������������ߵĶԳ���x=-��y���Ҳ࣬�����ж�a��b��ţ��ɴ�ȷ������ȷ��
����������x������������õ�b2-4ac��0���������߹��㣨0��1�����ó�c=1���ɴ��ж�����ȷ��
��a-b+c=0����b��0�ó�a+b+c=2b��0����b��1��c=1��a��0���ó�a+b+c��a+1+1��2���ɴ��ж�����ȷ��
�������߹��㣨-1��0�����ó�a-b+c=0����a=b-1����a��0�ó�... ��10��ѧ����6��4Ů������С��ΪŮ�����У���ѡ6�˲μӡ�����֪ʶ�����������涨����ѡ3�ˣ���ѡ��С�������¼�Ӧ����____��ѡ���Ȼ�¼����������¼�������¼�������
 ����¼�
�������������¼������Ŀ����Դ�С�ж���Ӧ�¼������ͼ��ɣ�
��𣺡�������
������¼���ָ��һ�������£����ܷ���Ҳ���ܲ��������¼�����
��10��ѧ����6��4Ů������С��ΪŮ�����У���ѡ6�˲μӡ�����֪ʶ��������
���涨����ѡ3�ˣ���Ů��Ҳѡ3�ˣ���ѡ��С�����Ŀ����Դ���һ��������
�ʴ�Ϊ������¼���
����¼�
�������������¼������Ŀ����Դ�С�ж���Ӧ�¼������ͼ��ɣ�
��𣺡�������
������¼���ָ��һ�������£����ܷ���Ҳ���ܲ��������¼�����
��10��ѧ����6��4Ů������С��ΪŮ�����У���ѡ6�˲μӡ�����֪ʶ��������
���涨����ѡ3�ˣ���Ů��Ҳѡ3�ˣ���ѡ��С�����Ŀ����Դ���һ��������
�ʴ�Ϊ������¼��� ��a��ʵ����|a|��0����һ�¼��ǣ�����
A. ��Ȼ�¼� B. ��ȷ���¼� C. �������¼� D. ����¼�
 A
����������������
��a����������|a|��0���������⣬����a����������|a|��0����һ�¼��DZ�Ȼ�¼���
��ѡA��
A
����������������
��a����������|a|��0���������⣬����a����������|a|��0����һ�¼��DZ�Ȼ�¼���
��ѡA�� ��ͼ�������2����������˩һ��������һ��������ǧ.˩���ӵĵط������߶���2.5�ף�������Ȼ�´���������״������1��С����Ͻ����ǿ���0.5��ʱ��ͷ���պýӴ������ӣ������ӵ���͵�����ľ���Ϊ ��.

 0.5
����������������������Ե������ڵ�ֱ��Ϊx�ᣬ��͵����ڵ�ֱ��Ϊy�Ὠ��ƽ��ֱ������ϵ��Ȼ��������κ����Ľ���ʽ����������������꣬�����������������Ǿ������ľ���.
0.5
����������������������Ե������ڵ�ֱ��Ϊx�ᣬ��͵����ڵ�ֱ��Ϊy�Ὠ��ƽ��ֱ������ϵ��Ȼ��������κ����Ľ���ʽ����������������꣬�����������������Ǿ������ľ���. ������y=x2��5x+6��x�ύ��A��B���㣬��AB�ij�Ϊ__��
 1
�������������������y=0����0=x2��5x+6��
��ã�x1=2��x2=3��
��AB�ij���3��2=1��
1
�������������������y=0����0=x2��5x+6��
��ã�x1=2��x2=3��
��AB�ij���3��2=1�� 
