题目内容
将抛物线y=x2﹣4x+4沿y轴向下平移9个单位，所得新抛物线与x轴正半轴交于点B，与y轴交于点C，顶点为D．求：（1）点B、C、D坐标；（2）△BCD的面积．
（1）（5，0）；（2）15.
【解析】试题分析：
（1）先由图象平移的规律求出抛物线的解析式，配方后可得顶点D的坐标，设y=0，可得B的坐标，设x=0，可得C的坐标；
（2）过D作DA⊥y轴于点A，根据图形的面积的和与差求△BCD的面积.
试题解析：
（1）抛物线y=x2﹣4x+4沿y轴向下平移9个单位后解析式是y=x2﹣4x+4﹣9，即y=x2﹣4x﹣5．
...
四边形ABCD中，对角线AC、BD相交于点O，给出下列四个条件：
①AD∥BC；②AD=BC；③OA=OC；④OB=OD
从中任选两个条件，能使四边形ABCD为平行四边形的选法有（ ）
A. 3种 B. 4种 C. 5种 D. 6种
B
【解析】试题分析：①②组合可根据一组对边平行且相等的四边形是平行四边形判定出四边形ABCD为平行四边形；
③④组合可根据对角线互相平分的四边形是平行四边形判定出四边形ABCD为平行四边形；
①③可证明△ADO≌△CBO，进而得到AD＝CB，可利用一组对边平行且相等的四边形是平行四边形判定出四边形ABCD为平行四边形；
①④可证明△ADO≌△CBO，进而得到AD＝CB，可... 如图，四边形ABCD中，AD∥BC，AE⊥AD交BD于点E，CF⊥BC交BD于点F，且AE=CF，求证：四边形ABCD是平行四边形．
证明见解析.
【解析】试题分析：根据AAS可证明Rt△AED≌Rt△CFB，得到AD=BC，利用一组对边平行且相等的四边形是平行四边形可判断四边形ABCD是平行四边形.
试题解析：∵AE⊥AD，CF⊥BC，∴∠EAD=∠FCB=90°，∵AD∥BC，∴∠ADE=∠CBF，在Rt△AED和Rt△CFB中，∵，∴Rt△AED≌Rt△CFB（AAS），∴AD=BC，∵AD∥BC，∴四边形AB... 一个多边形的外角和与它的内角和相等，则多边形是( )
A. 三角形 B. 四边形 C. 五边形 D. 六边形
B
【解析】多边形外角和为，内角和为，
，
，
所以该多边形为四边形． 如图，已知抛物线y=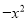
+mx+3与x轴交于A，B两点，与y轴交于点C，点B的坐标为（3，0），
（1）求m的值及抛物线的顶点坐标．
（2）点P是抛物线对称轴l上的一个动点，当PA+PC的值最小时，求点P的坐标．
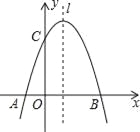
(1)m=2,(1,4)；(2)（1,2）.
【解析】试题分析：（1）首先把点B的坐标为（3，0）代入抛物线y=+mx+3，利用待定系数法即可求得m的值，继而求得抛物线的顶点坐标；
（2）首先连接BC交抛物线对称轴l于点P，则此时PA+PC的值最小，然后利用待定系数法求得直线BC的解析式，继而求得答案．
试题解析：（1）把点B的坐标为（3，0）代入抛物线y=+mx+3得：0=+3... 如图，已知二次函数y=ax2+bx+c（a≠0）的图象与x轴交于点A（﹣1，0），与y轴的交点B在（0，﹣2）和（0，﹣1）之间（不包括这两点），对称轴为直线x=1．下列结论：①abc＞0 ②4a+2b+c＞0 ③4ac﹣b2＜8a ④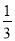
＜a＜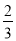
⑤b＞c．其中含所有正确结论的选项是（ ）
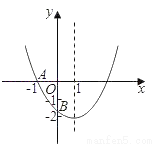
A. ①③ B. ①③④ C. ②④⑤ D. ①③④⑤
D
【解析】试题分析：①∵函数开口方向向上，∴a＞0；∵对称轴在y轴右侧，∴ab异号，∵抛物线与y轴交点在y轴负半轴，∴c＜0，∴abc＞0，故①正确；②∵图象与x轴交于点A（﹣1，0），对称轴为直线x=1，∴图象与x轴的另一个交点为（3，0），∴当x=2时，y＜0，∴4a+2b+c＜0，故②错误；③∵图象与x轴交于点A（﹣1，0），∴当x=﹣1时，y= =0，∴a﹣b+c=0，即a=b﹣c... 下列抛物线中，与抛物线y=x2﹣2x+4具有相同对称轴的是（ ）
A. y=4x2+2x+1 B. y=2x2﹣4x+1 C. y=2x2﹣x+4 D. y=x2﹣4x+2
B
【解析】【解析】
抛物线y=x2﹣2x+4的对称轴为x=1；
A、y=4x2+2x+1的对称轴为x=﹣，不符合题意；
B、y=2x2﹣4x+1的对称轴为x=1，符合题意；
C、y=2x2﹣x+4的对称轴为x=，不符合题意；
D、y=x2﹣4x+2的对称轴为x=2，不符合题意；
故选B． 用十个球设计一个游戏，使摸到红球、白球的可能性相同，并且摸到黄球的可能性比摸到红球的可能性小．
红球4个，白球4个，黄球2个.
【解析】试题分析：此题要想使摸到红球、白球的可能性相同，摸到黄球的可能性比摸到红球的可能性小，只要红球、白球个数相同，红球的个数多于黄球的个数即可．
试题解析：由题意知共10个球，即红球个数+白球个数+黄球个数＝10
摸到红球、白球的可能性相同
∴红球个数=白球个数=1，2，3，4
∴红球个数，白球个数，黄球个数可能是:1，1，8或2，... 如图，将矩形ABCD绕点A顺时针旋转到矩形AB′C′D′的位置，旋转角为α（0°＜α＜90°），若∠1=110°，则∠α= ．
。
【解析】试题分析：根据矩形的性质得∠B=∠D=∠BAD=90°，根据旋转的性质得∠D′=∠D=90°，∠4=α，利用对顶角相等得到∠1=∠2=110°，再根据四边形的内角和为360°可计算出∠3=70°，然后利用互余即可得到∠α的度数．
【解析】
如图，
∵四边形ABCD为矩形，
∴∠B=∠D=∠BAD=90°，
∵矩形ABCD绕点A顺时针旋转得到矩形AB′C′...