题目内容
“a是实数，|a|≥0”这一事件是（ ）
A. 必然事件 B. 不确定事件 C. 不可能事件 D. 随机事件
A
【解析】【解析】
“a是有理数，|a|≥0”是真命题，即“a是有理数，|a|≥0”这一事件是必然事件．
故选A．
练习册系列答案
相关题目
如图，四边形ABCD中，AD∥BC，AE⊥AD交BD于点E，CF⊥BC交BD于点F，且AE=CF，求证：四边形ABCD是平行四边形．
证明见解析.
【解析】试题分析：根据AAS可证明Rt△AED≌Rt△CFB，得到AD=BC，利用一组对边平行且相等的四边形是平行四边形可判断四边形ABCD是平行四边形.
试题解析：∵AE⊥AD，CF⊥BC，∴∠EAD=∠FCB=90°，∵AD∥BC，∴∠ADE=∠CBF，在Rt△AED和Rt△CFB中，∵，∴Rt△AED≌Rt△CFB（AAS），∴AD=BC，∵AD∥BC，∴四边形AB... 下列抛物线中，与抛物线y=x2﹣2x+4具有相同对称轴的是（ ）
A. y=4x2+2x+1 B. y=2x2﹣4x+1 C. y=2x2﹣x+4 D. y=x2﹣4x+2
B
【解析】【解析】
抛物线y=x2﹣2x+4的对称轴为x=1；
A、y=4x2+2x+1的对称轴为x=﹣，不符合题意；
B、y=2x2﹣4x+1的对称轴为x=1，符合题意；
C、y=2x2﹣x+4的对称轴为x=，不符合题意；
D、y=x2﹣4x+2的对称轴为x=2，不符合题意；
故选B． 用十个球设计一个游戏，使摸到红球、白球的可能性相同，并且摸到黄球的可能性比摸到红球的可能性小．
红球4个，白球4个，黄球2个.
【解析】试题分析：此题要想使摸到红球、白球的可能性相同，摸到黄球的可能性比摸到红球的可能性小，只要红球、白球个数相同，红球的个数多于黄球的个数即可．
试题解析：由题意知共10个球，即红球个数+白球个数+黄球个数＝10
摸到红球、白球的可能性相同
∴红球个数=白球个数=1，2，3，4
∴红球个数，白球个数，黄球个数可能是:1，1，8或2，... 玉树地震灾区小朋友卓玛从某地捐赠的2种不同款式的书包和2种不同款式的文具盒中，分别取一个书包和一个文具盒进行款式搭配，则不同搭配的可能有__种．
4
【解析】【解析】
每种书包有2种不同款式的文具盒搭配，2种书包就有2×2=4种搭配方式 抛掷一个质地均匀且六个面上依次刻有1-6的点数的正方体型骰子，抛掷后，观察向上的一面的点数，下列情况属必然事件的是（ ）
A. 出现的点数是偶数 B. 出现的点数不会是0
C. 出现的点数是2 D. 出现的点数为奇数
B
【解析】试题解析：因为正方体型骰子质地均匀且有六个面，抛掷落地后，每一个面都有可能朝上，但一定不可能出现0.
故选B. 下列说法正确的是（ ）
A. 随机事件发生的可能性是50%
B. 确定事件发生的可能性是1
C. 为了了解岳阳5万名学生中考数学成绩，可以从中抽取10名学生作为样本
D. 确定事件发生的可能性是0或1
D
【解析】试题解析：对于A，随机事件发生的可能性大于0，而小于100%，是在一个范围之内，并不是一个确定的数值；对于B，确定事件，包括发生的可能性是0或1；对于C，应该是从中抽取10名学生的中考数学成绩作为一个样本；D是在B的基础上完整叙述，正确.
故选D. 如图，将矩形ABCD绕点A顺时针旋转到矩形AB′C′D′的位置，旋转角为α（0°＜α＜90°），若∠1=110°，则∠α= ．
。
【解析】试题分析：根据矩形的性质得∠B=∠D=∠BAD=90°，根据旋转的性质得∠D′=∠D=90°，∠4=α，利用对顶角相等得到∠1=∠2=110°，再根据四边形的内角和为360°可计算出∠3=70°，然后利用互余即可得到∠α的度数．
【解析】
如图，
∵四边形ABCD为矩形，
∴∠B=∠D=∠BAD=90°，
∵矩形ABCD绕点A顺时针旋转得到矩形AB′C′... 如图，等边三角形ABD和等边三角形CBD的边长均为a，现把它们拼合起来，E是AD上异于A、D两点的一动点，F是CD上一动点，满足AE+CF=a．则△BEF的形状如何？
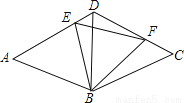
△BEF为正三角形，理由见解析
【解析】试题分析：根据已知条件易证△BDE≌△BCF，即可求得∠FBD+∠DBE=60°，根据一个内角为60°的等腰三角形可以判定为等边三角形，即可得结论．
试题解析：
△BEF为正三角形
证明：∵AE+CF=a，AE+ED=a，
∴DE=CF，
在△BDE和△BCF中，
∴△BDE≌△BCF，
∴BE=BF，∠CBF...