题目内容
从10名学生（6男4女，其中小芳为女生）中，抽选6人参加“防震知识”竞赛．若规定男生选3人，则“选到小芳”的事件应该是____（选填“必然事件、不可能事件、随机事件”）．
随机事件
【解析】根据事件发生的可能性大小判断相应事件的类型即可．
解答：【解析】
“随机事件是指在一定条件下，可能发生也可能不发生的事件”，
从10名学生（6男4女，其中小芳为女生）中，抽选6人参加“防震知识”竞赛．
若规定男生选3人，则女生也选3人，“选到小芳”的可能性大，但不一定发生．
故答案为：随机事件．
名校课堂系列答案如图是一个由5张纸片拼成的平行四边形，相邻纸片之间互不重叠也无缝隙，其中两张等腰直角三角形纸片的面积都为S1，另两张直角三角形纸片的面积都为S2，中间一张正方形纸片的面积为S3，则这个平行四边形的面积一定可以表示为（ ）
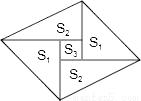
A. 4S1 B. 4S2 C. 4S2+S3 D. 3S1+4S3
A
【解析】试题分析：设等腰直角三角形的直角边长为a，中间小正方形的边长为b，则另两个直角三角形的边长分别为a-b，a+b，所以S1=，S2=，S3=，平行四边形的面积=2S1+2S2+S3=++=2=4S1，故答案选A. 如图，已知二次函数y=ax2+bx+c（a≠0）的图象与x轴交于点A（﹣1，0），与y轴的交点B在（0，﹣2）和（0，﹣1）之间（不包括这两点），对称轴为直线x=1．下列结论：①abc＞0 ②4a+2b+c＞0 ③4ac﹣b2＜8a ④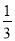
＜a＜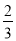
⑤b＞c．其中含所有正确结论的选项是（ ）
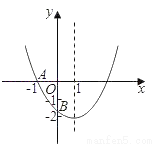
A. ①③ B. ①③④ C. ②④⑤ D. ①③④⑤
D
【解析】试题分析：①∵函数开口方向向上，∴a＞0；∵对称轴在y轴右侧，∴ab异号，∵抛物线与y轴交点在y轴负半轴，∴c＜0，∴abc＞0，故①正确；②∵图象与x轴交于点A（﹣1，0），对称轴为直线x=1，∴图象与x轴的另一个交点为（3，0），∴当x=2时，y＜0，∴4a+2b+c＜0，故②错误；③∵图象与x轴交于点A（﹣1，0），∴当x=﹣1时，y= =0，∴a﹣b+c=0，即a=b﹣c... 如图，是二次函数y=ax2+bx+c图象的一部分，其对称轴为直线x=1，若其与x轴一交点为A（3，0），则由图象可知，不等式ax2+bx+c＜0的解集是_____．
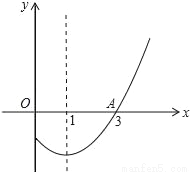
﹣1＜x＜3
【解析】试题分析：根据二次函数的性质可得：二次函数与x轴的另一个交点坐标为(-1，0)，则根据二次函数的图像可得：不等式的解集为. 用十个球设计一个游戏，使摸到红球、白球的可能性相同，并且摸到黄球的可能性比摸到红球的可能性小．
红球4个，白球4个，黄球2个.
【解析】试题分析：此题要想使摸到红球、白球的可能性相同，摸到黄球的可能性比摸到红球的可能性小，只要红球、白球个数相同，红球的个数多于黄球的个数即可．
试题解析：由题意知共10个球，即红球个数+白球个数+黄球个数＝10
摸到红球、白球的可能性相同
∴红球个数=白球个数=1，2，3，4
∴红球个数，白球个数，黄球个数可能是:1，1，8或2，... 袋子中装有4个黑球和2个白球，这些球的形状、大小、质地等完全相同，在看不到球的条件下，随机地从袋子中摸出三个球．下列事件是必然事件的是（ ）
A. 摸出的三个球中至少有一个球是黑球 B. 摸出的三个球中至少有一个球是白球
C. 摸出的三个球中至少有两个球是黑球 D. 摸出的三个球中至少有两个球是白球
A
【解析】试题分析：必然事件是指事件发生的概率为1． 抛掷一个质地均匀且六个面上依次刻有1-6的点数的正方体型骰子，抛掷后，观察向上的一面的点数，下列情况属必然事件的是（ ）
A. 出现的点数是偶数 B. 出现的点数不会是0
C. 出现的点数是2 D. 出现的点数为奇数
B
【解析】试题解析：因为正方体型骰子质地均匀且有六个面，抛掷落地后，每一个面都有可能朝上，但一定不可能出现0.
故选B. 如图，有一抛物线拱桥，当水位线在AB位置时，拱桥顶离水面2m，水面宽4m，水面下降1m后，水面宽为( )
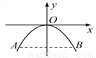
A. 5m B. 6m C.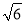 
m D. 2
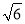m
D
【解析】试题分析：建立如图所示的坐标系，则点A的坐标为（-2，-2），设函数关系式为，则-2=4a，所以a= -，所以，当y=-3时， ，所以水面宽为m，故选：D． 根据下列表格对应值：
x | 3 | 4 | 5 |
y=ax2+bx+c | 0.5 | ﹣0.5 | ﹣1 |
判断关于x的方程ax2+bx+c=0（a≠0）的一个解x的范围是（ ）
A. x＜3 B. x＞5 C. 3＜x＜4 D. 4＜x＜5
C
【解析】试题分析：∵x=3时，y=0.5，即ax2+bx+c＞0；
x=4时，y=﹣0.5，即ax2+bx+c＜0，
∴抛物线与x轴的一个交点在（3，0）和（4，0）之间，
∴关于x的方程ax2+bx+c=0（a≠0）的一个解x的范围是3＜x＜4．
故选C．