题目内容
9. 已知a,b,c在数轴上对应点的位置如图.化简|a|-|a+b|+$\sqrt{(c-a)^{2}}$+|b-c|-|b|.
已知a,b,c在数轴上对应点的位置如图.化简|a|-|a+b|+$\sqrt{(c-a)^{2}}$+|b-c|-|b|.
分析 根据数轴得出b<a<0<c,|b|>|a|>|c|,求出a-b>0,c-a>0,b-c<0,根据二次根式的性质和绝对值得出-a-(a-b)+(c-a)-(c-b)-(-b),去括号后合并即可.
解答 解:∵从数轴可知:b<a<0<c,|b|>|a|>|c|,
∴a-b>0,c-a>0,b-c<0,
∴|a|-|a+b|+$\sqrt{(c-a)^{2}}$+|b-c|-|b|.
=-a-(a-b)+(c-a)-(c-b)-(-b)
=-a-a+b+c-a-c+b+b
=-3a+3b.
点评 本题考查了二次根式的性质,绝对值,数轴的应用,解此题的关键是求出原式=-a-(a-b)+(c-a)-(c-b)-(-b),题目比较典型,难度适中.

练习册系列答案
相关题目
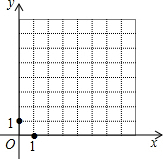 如图,在平面直角坐标系中,点P从原点O出发,每次向上平移2个单位长度或向右平移1个单位长度.平移1次后,可能到达的点的坐标是(0,2)、(1,0),这些点在函数y=-2x+2的图象上;平移2次后,可能到达的点的坐标是(0,4)、(1,2)、(2,0),这些点在函数y=-2x+4的图象上;平移3次后,可能到达的点的坐标是(0,6)、(1,4)、(2,2)、(3,0),这些点在函数y=-2x+6的图象上.
如图,在平面直角坐标系中,点P从原点O出发,每次向上平移2个单位长度或向右平移1个单位长度.平移1次后,可能到达的点的坐标是(0,2)、(1,0),这些点在函数y=-2x+2的图象上;平移2次后,可能到达的点的坐标是(0,4)、(1,2)、(2,0),这些点在函数y=-2x+4的图象上;平移3次后,可能到达的点的坐标是(0,6)、(1,4)、(2,2)、(3,0),这些点在函数y=-2x+6的图象上.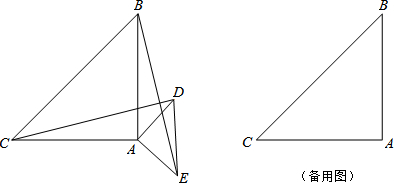
 如图,在平行四边形ABCD中,AE⊥BC于E,AF⊥CD于F,∠EAF=45°,且AE+AF=2$\sqrt{3}$,则平行四边形的周长4$\sqrt{6}$.
如图,在平行四边形ABCD中,AE⊥BC于E,AF⊥CD于F,∠EAF=45°,且AE+AF=2$\sqrt{3}$,则平行四边形的周长4$\sqrt{6}$.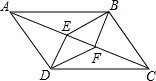 如图,?ABCD中,DE⊥AC,BF⊥AC,垂足分别为E、F,求证:BE∥DF.
如图,?ABCD中,DE⊥AC,BF⊥AC,垂足分别为E、F,求证:BE∥DF.