题目内容
17.计算:$\frac{1-\frac{1}{2}+\frac{1}{3}-\frac{1}{4}+\frac{1}{5}-\frac{1}{6}+…+\frac{1}{19}-\frac{1}{20}}{\frac{1}{11×20}+\frac{1}{12×19}+\frac{1}{13×18}+\frac{1}{14×17}+\frac{1}{15×16}}$.分析 把分母的分数进行拆项,再把分子中的项通过补项向分母的项靠拢,即可解答.
解答 解:∵原式的分子=(1-$\frac{1}{2}$+$\frac{1}{3}$-$\frac{1}{4}$+$\frac{1}{5}$-…-$\frac{1}{10}$-$\frac{2}{12}$-$\frac{2}{14}$-$\frac{2}{16}$-$\frac{2}{18}$-$\frac{2}{20}$)+$\frac{1}{11}$+$\frac{1}{12}$+$\frac{1}{13}$+…+$\frac{1}{20}$
=(1-$\frac{1}{2}$+$\frac{1}{3}$-$\frac{1}{4}$+$\frac{1}{5}$-…-$\frac{1}{10}$-$\frac{1}{6}$-$\frac{1}{7}$-$\frac{1}{8}$-$\frac{1}{9}$-$\frac{1}{10}$)+$\frac{1}{11}$+$\frac{1}{12}$+$\frac{1}{13}$+…+$\frac{1}{20}$
=$\frac{1}{11}$+$\frac{1}{12}$+$\frac{1}{13}$+…+$\frac{1}{20}$
原式的分母=$\frac{1}{31}$($\frac{1}{11}$+$\frac{1}{20}$+$\frac{1}{12}$+$\frac{1}{19}$+…+$\frac{1}{15}$+$\frac{1}{15}$)=$\frac{1}{31}$($\frac{1}{11}$+$\frac{1}{12}$+$\frac{1}{13}$+…+$\frac{1}{20}$)
∴原式=31.
点评 本题考查了有理数的混合运算,解决本题的关键是把分母中的分数进行拆项,把分子进行补项,最后分子与分母进行约分即可解答.

 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案| A. | y3<y1<y2 | B. | y1<y2<y3 | C. | y2<y3<y1 | D. | y2<y1<y3 |
| A. |  | B. |  | C. |  | D. |  |
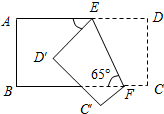 如图,把一张长方形纸片沿EF折叠后,点D、C分别落在D′,C′的位置,若∠EFB=65°,求∠AED′和∠BFC′的度数.
如图,把一张长方形纸片沿EF折叠后,点D、C分别落在D′,C′的位置,若∠EFB=65°,求∠AED′和∠BFC′的度数. 如图,在Rt△ABC中,∠C=90°,BD平分∠ABC,交AC于点D,DE⊥AB,E为AB的中点,且DE=10cm,则AC=30cm.
如图,在Rt△ABC中,∠C=90°,BD平分∠ABC,交AC于点D,DE⊥AB,E为AB的中点,且DE=10cm,则AC=30cm. 已知a,b,c在数轴上对应点的位置如图.化简|a|-|a+b|+$\sqrt{(c-a)^{2}}$+|b-c|-|b|.
已知a,b,c在数轴上对应点的位置如图.化简|a|-|a+b|+$\sqrt{(c-a)^{2}}$+|b-c|-|b|.