题目内容
 如图,五边形ABCDE中,AB=AE,BC=DE,∠B=∠E,且F点为CD边上中点.
如图,五边形ABCDE中,AB=AE,BC=DE,∠B=∠E,且F点为CD边上中点.(1)求证:AF⊥CD;
(2)连接BE,不再添加任何字母的情况下,你还能得到哪些正确结论?试写出你认为正确的两个结论,不需证明.
考点:全等三角形的判定与性质
专题:
分析:(1)连接AC,AD,可证明△ABC≌△AED,进而得到AC=AD,再利用等腰三角形的性质:三线合一即可得到AF⊥CD.
(2)连接BE,可得△ABE是等腰三角形,然后根据等腰三角形的性质可得∠ABE=∠AEB,再根据等式的性质可得∠CBE=∠DEB.
(2)连接BE,可得△ABE是等腰三角形,然后根据等腰三角形的性质可得∠ABE=∠AEB,再根据等式的性质可得∠CBE=∠DEB.
解答: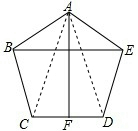 (1)证明:证明:连接AC,AD,
(1)证明:证明:连接AC,AD,
在△ABC和△AED中,
∴△ABC≌△AED(SAS),
∴AC=AD,
∵点F是CD的中点,
∴AF⊥CD.
(2)解:连接BE,∵AB=AE,
∴∠ABE=∠AEB,
∵∠ABC=∠AED,
∴∠CBE=∠DEB.
 (1)证明:证明:连接AC,AD,
(1)证明:证明:连接AC,AD,在△ABC和△AED中,
|
∴△ABC≌△AED(SAS),
∴AC=AD,
∵点F是CD的中点,
∴AF⊥CD.
(2)解:连接BE,∵AB=AE,
∴∠ABE=∠AEB,
∵∠ABC=∠AED,
∴∠CBE=∠DEB.
点评:此题主要考查了全等三角形的判定与性质,以及等腰三角形的性质,关键是掌握全等三角形的判定方法.

练习册系列答案
相关题目
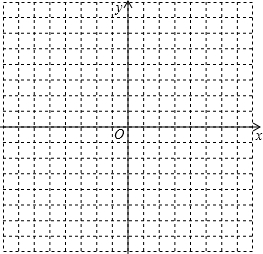 建立直角坐标系,标出以下各组点,并将各组内的点用线段依次连接起来,观察所得的图形,你认为它是什么?
建立直角坐标系,标出以下各组点,并将各组内的点用线段依次连接起来,观察所得的图形,你认为它是什么?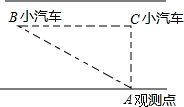 “交通管理条例”规定:小汽车在城街路上行驶速度不得超过70千米/小时,如图,一辆小汽车在一条城市街路上直道行驶,某一时刻刚好行驶到路面车速检测仪A的正前方30米C处,过了2秒后,测得小汽车在B处与车速检测仪间距离为50米,这辆小汽车超速了吗?
“交通管理条例”规定:小汽车在城街路上行驶速度不得超过70千米/小时,如图,一辆小汽车在一条城市街路上直道行驶,某一时刻刚好行驶到路面车速检测仪A的正前方30米C处,过了2秒后,测得小汽车在B处与车速检测仪间距离为50米,这辆小汽车超速了吗?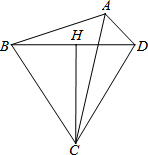 已知:四边形ABCD中,∠ABC+∠ADC=180°,CH垂直平分BD
已知:四边形ABCD中,∠ABC+∠ADC=180°,CH垂直平分BD 如图,∠A=60°,∠ABO=28°,∠ACO=30°,则∠BOC=
如图,∠A=60°,∠ABO=28°,∠ACO=30°,则∠BOC=