题目内容
16.(1)$\frac{\sqrt{24}+\sqrt{3}}{\sqrt{3}}$-(3-π)0(2)$\sqrt{12}$$-\root{3}{-8}$$+\sqrt{27}$$-\sqrt{18}$$+\sqrt{75}$
(3)4x2-49=0
(4)(x+2)3+1=$\frac{7}{8}$.
分析 (1)原式利用二次根式的除法法则及零指数幂法则计算,即可得到结果;
(2)原式利用立方根及二次根式性质化简,计算即可得到结果;
(3)方程整理后,利用平方根定义计算即可求出解;
(4)方程整理后,利用立方根定义开立方即可求出解.
解答 解:(1)原式=$\sqrt{8}$+1-1=2$\sqrt{2}$;
(2)原式=2$\sqrt{3}$+2+3$\sqrt{3}$-3$\sqrt{2}$+5$\sqrt{3}$=10$\sqrt{3}$-3$\sqrt{2}$+2;
(3)方程整理得:x2=$\frac{49}{4}$,
开方得:x=±$\frac{7}{2}$;
(4)方程整理得:(x+2)3=-$\frac{1}{8}$,
开立方得:x+2=-$\frac{1}{2}$,
解得:x=-2$\frac{1}{2}$.
点评 此题考查了实数的运算,熟练掌握运算法则是解本题的关键.

练习册系列答案
相关题目
7.如果(x2+px+q)(x2+7)的展开式中不含x2与x3的项,那以p,q的值是( )
| A. | p=1,q=7 | B. | p=0,q=-7 | C. | p=2,q=1 | D. | p=0,q=7 |
4.在-22,-(-2),+(-$\frac{1}{2}$),-|-2|这四个数中,负数的个数是( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
1.估算$\sqrt{18}$的值在( )
| A. | 在1和2之间 | B. | 在2和3之间 | C. | 在3和4之间 | D. | 在4和5之间 |
8.下列说法正确的是( )
| A. | -5是25的平方根 | B. | 25的平方根是-5 | ||
| C. | $\sqrt{16}$是$\root{3}{-27}$的算术平方根 | D. | $\sqrt{3}$是$\sqrt{{{(-3)}^2}}$的算术平方根 |
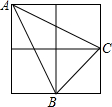 如图,由四个边长为1的小正方形构成一个大正方形,连结小正方形的三个顶点,可得到△ABC,则△ABC中AB边上的高是$\frac{3\sqrt{5}}{5}$.
如图,由四个边长为1的小正方形构成一个大正方形,连结小正方形的三个顶点,可得到△ABC,则△ABC中AB边上的高是$\frac{3\sqrt{5}}{5}$.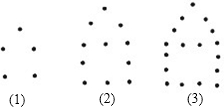 如图所示,摆第一个“小屋子”要5枚棋子,摆第二个要11枚棋子,摆第三个要17枚棋子,摆第四个要23枚棋子,摆第30个“小屋子”要179枚棋子.
如图所示,摆第一个“小屋子”要5枚棋子,摆第二个要11枚棋子,摆第三个要17枚棋子,摆第四个要23枚棋子,摆第30个“小屋子”要179枚棋子.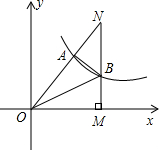 如图,双曲线y=$\frac{k}{x}$经过Rt△OMN斜边上的点A,与直角边MN相交于点B,若OA=2AN,且△OAB的面积恰是方程(2-$\sqrt{3}$)x2-4($\sqrt{3}$-1)x-10=0的根,则k的值是12($\sqrt{3}$+1).
如图,双曲线y=$\frac{k}{x}$经过Rt△OMN斜边上的点A,与直角边MN相交于点B,若OA=2AN,且△OAB的面积恰是方程(2-$\sqrt{3}$)x2-4($\sqrt{3}$-1)x-10=0的根,则k的值是12($\sqrt{3}$+1).