题目内容
如图,在平面直角坐标系中,O为坐标原点,抛物线y=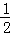 x2+2x与x轴相交于O、B,顶点为A,连接OA.
x2+2x与x轴相交于O、B,顶点为A,连接OA.
(1)A的坐标 ,∠AOB= 。
(2)若将抛物线y= x2+2x向右平移4个单位,再向下平移2个单位,得到抛物线m,其顶点为点C.连接OC和AC,把△AOC沿OA翻折得到四边形ACOC′.试判断其形状,并说明理由;
x2+2x向右平移4个单位,再向下平移2个单位,得到抛物线m,其顶点为点C.连接OC和AC,把△AOC沿OA翻折得到四边形ACOC′.试判断其形状,并说明理由;
(3)在(2)的情况下,判断点C′是否在抛物线y= x2+2x上,请说明理由;
x2+2x上,请说明理由;
(4)若点P为x轴上的一个动点,试探究在抛物线m上是否存在点Q,使以点O、P、C、Q为顶点的四边形是平行四边形,且OC为该四边形的一条边?若存在,请直接写出点Q的坐标;若不存在,请说明理由.
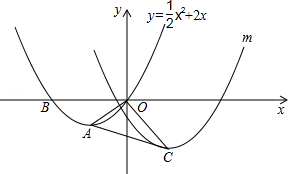
(1)(-2,-2);45°(2分)(2)四边形ACOC′为菱形.(1分)
由题意可知抛物线m的二次项系数为 ,且过顶点C的坐标是(2,﹣4),
,且过顶点C的坐标是(2,﹣4),
∴抛物线的解析式为:y= (x﹣2)2﹣4,即y=
(x﹣2)2﹣4,即y= x2﹣2x﹣2,(1分)
x2﹣2x﹣2,(1分)
过点C作CE⊥x轴,垂足为E;过点A作AF⊥CE,垂足为F,与y轴交与点H,
 ∴OE=2,CE=4,AF=4,CF=CE﹣EF=2,
∴OE=2,CE=4,AF=4,CF=CE﹣EF=2,
∴OC= =
= =2
=2 ,
,
同理,AC=2 ,OC=AC,
,OC=AC,
由反折不变性的性质可知,OC=AC=OC′=AC′,
故四边形ACOC′为菱形.(1分)(共3分)
(3)如图1,点C′不在抛物线y= x2+2x上.(1分)
x2+2x上.(1分)
理由如下:
过点C′作C′G⊥x轴,垂足为G,
∵OC和OC′关于OA对称,∠AOB=∠AOH=45°,
∴∠COH=∠C′OG,
∵CE∥OH,
∴∠OCE=∠C′OG,
又∵∠CEO=∠C′GO=90°,OC=OC′,
∴△CEO≌△C′GO,
∴OG=4,C′G=2,
∴点C′的坐标为(﹣4,2),(1分)
把x=﹣4代入抛物线y= x2+2x得y=0,
x2+2x得y=0,
∴点C′不在抛物线y= x2+2x上;(1分)(共3分)
x2+2x上;(1分)(共3分)
(4)存在符合条件的点Q.
∵点P为x轴上的一个动点,点Q在抛物线m上,
∴设Q(a, (a﹣2)2﹣4),
(a﹣2)2﹣4),
∵OC为该四边形的一条边,
∴OP为对角线,
∴ =0,解得x1=6,x2=4,
=0,解得x1=6,x2=4,
∴P(6,4)或(﹣2,4)(舍去),
∴点Q的坐标为(6,4). (直接写出即可,2分,多写1个只得1分)
文澜中学的难度系数约0.76,全杭州市的难度系数约0.63

 中自变量x的取值范围是________.
中自变量x的取值范围是________.  ,求这个角。
,求这个角。
 ,∠B=60°,则CD的长为( )
,∠B=60°,则CD的长为( )
 D. 1
D. 1 自变量x的取值范围是
自变量x的取值范围是  从P点射出一束光线经0A上的Q点反射后,反射光线QR恰好与0B平行,则∠QPB的度数是( )
从P点射出一束光线经0A上的Q点反射后,反射光线QR恰好与0B平行,则∠QPB的度数是( )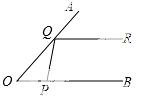
 AC的长为半径画弧,两弧交于P,Q两点;
AC的长为半径画弧,两弧交于P,Q两点; 交AB,AC于点E,D,连接CE;
交AB,AC于点E,D,连接CE;