题目内容
已知三条线段a,b,c,其长度分别为a=mn,b=
(m2+n2),c=
(m-n)2(其中m,n为不相等的正数),试问a,b,c三条线段能否构成三角形?请说明理由.
| 1 |
| 2 |
| 1 |
| 4 |
考点:因式分解的应用,三角形三边关系
专题:
分析:已知三边,应用第三边的长度大于两边的差而小于两边的和,从而根据已知数据可确定a,b,c三条线段能否构成三角形.
解答:解:a+b=mn+
(m2+n2)=
m2+
n2+mn=
(m2+n2+2mn)=
(m+n)2,b-a=
(m2+n2)-mn=
(m-n)2,
∵m,n为不相等的正数,
∴
(m+n)2>
( m-n)2,
(m-n)2<
( m-n)2;
∴a+b>c,b-a<c;
∴a,b,c三条线段能构成三角形.
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∵m,n为不相等的正数,
∴
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 2 |
| 1 |
| 4 |
∴a+b>c,b-a<c;
∴a,b,c三条线段能构成三角形.
点评:考查三角形的边时,要注意三角形形成的条件:任意两边之和>第三边,任意两边之差<第三边.

练习册系列答案
 七彩题卡口算应用一点通系列答案
七彩题卡口算应用一点通系列答案
相关题目
 如图,AB∥DE,那么∠BCD=( )
如图,AB∥DE,那么∠BCD=( )| A、∠2=∠1 |
| B、∠1+∠2 |
| C、180°+∠1-∠2 |
| D、180°+∠2-2∠1 |

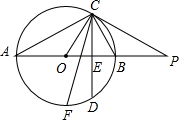 如图,AB是⊙O的直径,点C在⊙O上,过点C的直线与AB的延长线交于点P,∠COB=2∠PCB.
如图,AB是⊙O的直径,点C在⊙O上,过点C的直线与AB的延长线交于点P,∠COB=2∠PCB. 如图,某拦河坝横截面的原设计方案为梯形ABCD,其中AD∥BC,∠ABC=72°.为了提高拦河大坝的安全性,现将坝顶宽度水平缩短10m,坝底宽度水平增加4m,使∠EFC=45°.
如图,某拦河坝横截面的原设计方案为梯形ABCD,其中AD∥BC,∠ABC=72°.为了提高拦河大坝的安全性,现将坝顶宽度水平缩短10m,坝底宽度水平增加4m,使∠EFC=45°.