题目内容
在Rt△ABC中,CD是斜边AB上的高,如果AB=a,∠B=α,那么AD等于( )
| A、asin2α |
| B、acos2α |
| C、asinαcosα |
| D、asinαtanα |
考点:解直角三角形
专题:
分析:根据AB=a,∠B=α,可以求得BC的值,进而可以求得CD的值,根据CD即可求得AD的值,即可解题.
解答:解:如图,
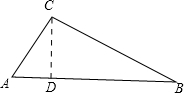
∵∠A+∠B=90°,∠A+∠ACD=90°,
∴∠ACD=∠B=α,
∵RT△ABC中,AB=a,∠B=α,
∴BC=a•cosα,
∵RT△BCD中,BC=a•cosα,∠B=α,
∴CD=a•cosα•sinα,
∵RT△ACD中,CD=a•cosα•sinα,∠ACD=α,
∴AD=CD•tan∠ACD=a•cosα•sinα•tanα=asinα•sinα.
故选A.

∵∠A+∠B=90°,∠A+∠ACD=90°,
∴∠ACD=∠B=α,
∵RT△ABC中,AB=a,∠B=α,
∴BC=a•cosα,
∵RT△BCD中,BC=a•cosα,∠B=α,
∴CD=a•cosα•sinα,
∵RT△ACD中,CD=a•cosα•sinα,∠ACD=α,
∴AD=CD•tan∠ACD=a•cosα•sinα•tanα=asinα•sinα.
故选A.
点评:本题考查了直角三角形中三角函数的运用,本题中求得CD的长是解题的关键.

练习册系列答案
相关题目

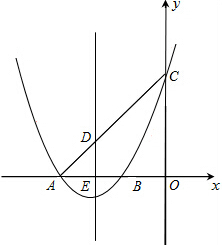 已知抛物线y=x2+4x+3交x轴于A、B两点,交y轴于点C,抛物线的对称轴交x轴于点E,求抛物线上是否存在点M,使直线CM把四边形DEOC分成面积相等的两部分?若存在,请写出M所在直线的解析式.
已知抛物线y=x2+4x+3交x轴于A、B两点,交y轴于点C,抛物线的对称轴交x轴于点E,求抛物线上是否存在点M,使直线CM把四边形DEOC分成面积相等的两部分?若存在,请写出M所在直线的解析式. 如图,AB、DC、CB分别与⊙O相切于E、F、G,且AB∥CD.
如图,AB、DC、CB分别与⊙O相切于E、F、G,且AB∥CD.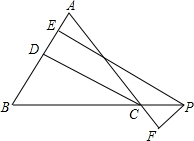 如图,在△ABC中,AB=AC,PE⊥AB,PF⊥AC,CD⊥AB,垂足分别为E、D、F,求证:PE-PF=CD.
如图,在△ABC中,AB=AC,PE⊥AB,PF⊥AC,CD⊥AB,垂足分别为E、D、F,求证:PE-PF=CD.