题目内容
有一座建筑物，在地面上A点测得其顶点C的仰角为30°，向建筑物前进50米到B点右侧的C点，测得顶点C的仰角为45°，求建筑的高度（结果精确到0.1米）
考点：解直角三角形的应用-仰角俯角问题
专题：
分析：首先分析图形：根据题意构造直角三角形；本题涉及到两个直角三角形△ADC、△ADB，应利用其公共边CD构造等量关系，借助AB=AD+BD构造方程关系式，进而可求出答案．
解答：
解：依题意，知∠A=30°，∠CBD=45°，AB=50米．
在Rt△ADC中，AD=CD•cot30°=
CD．
在Rt△CDB中，CD=BD，
∵AD+BD=50米，
∴
CD+CD=50，
解得 CD=25（
-1）≈18.3（米）．
答：建筑物的高度约为18.3米．
解：依题意，知∠A=30°，∠CBD=45°，AB=50米．在Rt△ADC中，AD=CD•cot30°=
| 3 |
在Rt△CDB中，CD=BD，
∵AD+BD=50米，
∴
| 3 |
解得 CD=25（
| 3 |
答：建筑物的高度约为18.3米．
点评：本题考查俯角、仰角的定义，要求学生能借助俯角、仰角构造直角三角形并结合图形利用三角函数解直角三角形．
练习册系列答案
相关题目
若x1，x2是方程x2-6x+3=0的两个根，则x1+x2的值为（ ）
| A、6 | B、-6 | C、3 | D、-3 |
如图，点D是BC的中点，点E是AC的中点，点F是AB的中点．如果AB=BC=AC，那么与BD（BD除外）相等的线段共有（ ）| A、6条 | B、5条 | C、4条 | D、3条 |
在Rt△ABC中，CD是斜边AB上的高，如果AB=a，∠B=α，那么AD等于（ ）
| A、asin2α |
| B、acos2α |
| C、asinαcosα |
| D、asinαtanα |
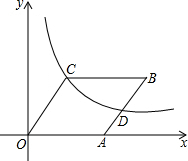如图，?OABC的顶点B、C在第一象限，点A的坐标为（3，0），D为边AB的中点，反比例函数y=