题目内容
 如图,AB、DC、CB分别与⊙O相切于E、F、G,且AB∥CD.
如图,AB、DC、CB分别与⊙O相切于E、F、G,且AB∥CD.(1)试判断BE、CF、BC之间的数量关系,并给予证明;
(2)连接OB、OC,试判断△BOC的形状,并给予证明.
考点:切线的性质,切线长定理
专题:
分析:(1)如图所示,连接OE、OG、OF;利用切线长定理进行证明BC=BE+CF;
(2)由切线长定理,易得∠OBE=∠OBF=
∠EBF,∠OCG=∠OCF=
∠GCF,又由AB∥CD,则可求得∠BOC=90°.
(2)由切线长定理,易得∠OBE=∠OBF=
| 1 |
| 2 |
| 1 |
| 2 |
解答: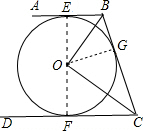 解:(1)BC=BE+CF.理由如下:
解:(1)BC=BE+CF.理由如下:
如图,连接OE、OG、OF.
∵AB、DC、CB分别与⊙O相切于点E、F、G,
∴BE=BG,CG=CF,
∴BC=BG+CG=BE+CF,即BC=BE+CF;
(2)△OBC是直角三角形.理由如下:
证明:∵AB、CD、BC分别与⊙O相切于点E、F、G,
∴∠OBE=∠OBF=
∠EBF,∠OCG=∠OCF=
∠GCF,
∵AB∥CD,
∴∠EBF+∠GCF=180°,
∴∠OBF+∠OCF=90°,
∴∠BOC=90°,
∴△OBC是直角三角形.
 解:(1)BC=BE+CF.理由如下:
解:(1)BC=BE+CF.理由如下:如图,连接OE、OG、OF.
∵AB、DC、CB分别与⊙O相切于点E、F、G,
∴BE=BG,CG=CF,
∴BC=BG+CG=BE+CF,即BC=BE+CF;
(2)△OBC是直角三角形.理由如下:
证明:∵AB、CD、BC分别与⊙O相切于点E、F、G,
∴∠OBE=∠OBF=
| 1 |
| 2 |
| 1 |
| 2 |
∵AB∥CD,
∴∠EBF+∠GCF=180°,
∴∠OBF+∠OCF=90°,
∴∠BOC=90°,
∴△OBC是直角三角形.
点评:此题考查了切线长定理、切线的性质以及直角三角形的判定与性质.此题难度适中,注意掌握数形结合思想的应用.

练习册系列答案
相关题目
在Rt△ABC中,CD是斜边AB上的高,如果AB=a,∠B=α,那么AD等于( )
| A、asin2α |
| B、acos2α |
| C、asinαcosα |
| D、asinαtanα |
 如图,AD是△ABC外接圆的直径,AD=6cm,∠DAC=∠ABC,求AC.
如图,AD是△ABC外接圆的直径,AD=6cm,∠DAC=∠ABC,求AC.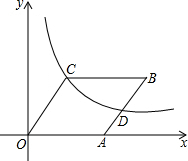 如图,?OABC的顶点B、C在第一象限,点A的坐标为(3,0),D为边AB的中点,反比例函数y=
如图,?OABC的顶点B、C在第一象限,点A的坐标为(3,0),D为边AB的中点,反比例函数y= 如图,OC是∠AOB内的一条射线,若∠BOC=
如图,OC是∠AOB内的一条射线,若∠BOC=