题目内容
7.计算:(1)$\frac{x+3y}{{x}^{2}-{y}^{2}}$-$\frac{x+2y}{{x}^{2}-{y}^{2}}$-$\frac{2x-3y}{{y}^{2}-{x}^{2}}$
(2)$\frac{1}{a+3}$-$\frac{6}{9-{a}^{2}}$.
(3)$\frac{{x}^{2}}{x-1}$-x-1
(4)($\frac{3x}{x+2}$-$\frac{x}{x-2}$)÷$\frac{2x}{{x}^{2}-4}$
(5)($\sqrt{\frac{5}{12}}$-2$\sqrt{3}$)×$\sqrt{15}$
(6)$\sqrt{8}$x+2x$\sqrt{2x}$-$\frac{1}{2}$$\sqrt{8{x}^{2}}$-4$\sqrt{\frac{x}{2}}$(x≥0)
分析 (1)原式变形后,利用同分母分式的加减法则计算即可得到结果;
(2)原式通分并利用同分母分式的加法法则计算即可得到结果;
(3)原式通分并利用同分母分式的减法法则计算即可得到结果;
(4)原式括号中两项通分并利用同分母分式的减法法则计算,同时利用除法法则变形,约分即可得到结果;
(5)原式利用二次根式的乘法法则计算,化简即可得到结果;
(6)原式各项化简后,合并即可得到结果.
解答 解:(1)原式=$\frac{x+3y-x-2y+2x-3y}{(x+y)(x-y)}$=$\frac{2(x-y)}{(x+y)(x-y)}$=$\frac{2}{x+y}$;
(2)原式=$\frac{a-3+6}{(a+3)(a-3)}$=$\frac{a+3}{(a+3)(a-3)}$=$\frac{1}{a-3}$;
(3)原式=$\frac{{x}^{2}-(x+1)(x-1)}{x-1}$=$\frac{1}{x-1}$;
(4)原式=$\frac{3{x}^{2}-6x-{x}^{2}-2x}{(x+2)(x-2)}$•$\frac{(x+2)(x-2)}{2x}$=$\frac{2x(x-4)}{2x}$=x-4;
(5)原式=$\sqrt{\frac{75}{12}}$-2$\sqrt{45}$=$\sqrt{\frac{25}{4}}$-6$\sqrt{5}$=$\frac{5}{2}$-6$\sqrt{5}$;
(6)原式=2$\sqrt{2}$x+2x$\sqrt{2x}$-$\sqrt{2}$x-2$\sqrt{2x}$=$\sqrt{2}$x.
点评 此题考查了分式的混合运算,以及二次根式的混合运算,熟练掌握运算法则是解本题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
16.某种细菌在培养过程中,每20分钟分裂一次(由1个分裂成2个),如果现在容器中有10个这种细菌,那么经过1小时后容器中的细菌个数为( )
| A. | 60 | B. | 80 | C. | 3×220 | D. | 10×220 |
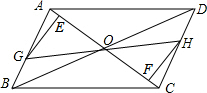 如图,在?ABCD中,点E、F在AC上,且AF=CE,GH过点O分别与AB、CD交于点G、H,试说明:
如图,在?ABCD中,点E、F在AC上,且AF=CE,GH过点O分别与AB、CD交于点G、H,试说明: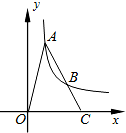 如图,A、B是双曲线y=$\frac{k}{x}$(k>0)上的点,A、B两点的横坐标分别是a、2a,线段AB的延长线交x轴于点C,若S△AOC=6.则k=( )
如图,A、B是双曲线y=$\frac{k}{x}$(k>0)上的点,A、B两点的横坐标分别是a、2a,线段AB的延长线交x轴于点C,若S△AOC=6.则k=( ) 如图由16个面积为1平方厘米的小正方形组成,求阴影部分的面积.
如图由16个面积为1平方厘米的小正方形组成,求阴影部分的面积.