题目内容
2．
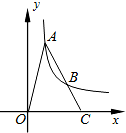如图，A、B是双曲线y=$\frac{k}{x}$（k＞0）上的点，A、B两点的横坐标分别是a、2a，线段AB的延长线交x轴于点C，若S△AOC=6．则k=（ ）| A． | 4 | B． | 3 | C． | 2 | D． | 1 |
分析 分别过点A、B作x轴的垂线，垂足分别为D、E，那么由AD∥BE，AD=2BE，可知B、E分别是AC、DC的中点，得出OC=3a，进而求出S△AOC=$\frac{1}{2}$AD×CO=$\frac{1}{2}$（a+2a）×$\frac{k}{a}$=$\frac{3k}{2}$=6，即可求出k的值．
解答 
解：分别过点A、B作x轴的垂线，垂足分别为D、E．
则AD∥BE，AD=2BE=$\frac{k}{a}$，
∴B、E分别是AC、DC的中点．
∴△ADC∽△BEC，
∵BE：AD=1：2，
∴EC：CD=1：2，
∴EC=DE=a，
∴OC=3a，
又∵A（a，$\frac{k}{a}$），B（2a，$\frac{k}{2a}$），
∴S△AOC=$\frac{1}{2}$AD×CO=$\frac{1}{2}$×3a×$\frac{k}{a}$=$\frac{3k}{2}$=6，
解得：k=4．
故选A．
点评 本题考查的是反比例函数系数k的几何意义，根据题意作出辅助线得出S△AOC=S梯形ACOF-S△AOF=6是解答此题的关键．
练习册系列答案
相关题目
如图所示，在?ABCD中，AB=2BC，点M是DC的中点，BE⊥AD，E是垂足，求证：∠EMC=3∠DEM．