题目内容
15.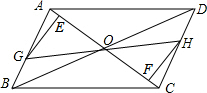 如图,在?ABCD中,点E、F在AC上,且AF=CE,GH过点O分别与AB、CD交于点G、H,试说明:
如图,在?ABCD中,点E、F在AC上,且AF=CE,GH过点O分别与AB、CD交于点G、H,试说明:(1)AG=CH;
(2)GH、EF互相平分.
分析 (1)根据平行四边形的性质得到∠BAC=∠ACD,AO=CO,证出△AOG≌△COH,根据全等三角形的性质即可得到结论.
(2)由平行四边形的性质得到对边平行,得到内错角相等,根据三角形全等,得到边相等,角相等,再由邻补角得到内错角相等,得到两线平行,然后根据平行四边形的性质和判定得到结论.
解答 证明:(1)在?ABCD中,
∵AB∥CD,
∴∠BAC=∠ACD,AO=CO,
在△AOG与△COH中,
$\left\{\begin{array}{l}{∠BAO=∠DCO}\\{AO=CO}\\{∠AOG=∠COD}\end{array}\right.$,
∴△AOG≌△COH,
∴AG=CH;
(2)在?ABCD中,
∵AB∥CD,
∴∠GAE=∠HCF,
∵AF=CE,
∴AF-EF=CE=EF,
即AE=CF,
在△AGE与△CHF中,
$\left\{\begin{array}{l}{AG=CH}\\{∠GAE=∠HCF}\\{AE=CF}\end{array}\right.$,
∴△AGE≌△CHF,
∴GE=HF,∠AEG=∠CFH,
∴∠GEO=∠HFO,
∴EG∥FH;
∴四边形GFHE是平行四边形,
∴GH、EF互相平分.
点评 本题考查了平行四边形的性质和判定,全等三角形的判定与性质,注意数形结合,分清平行四边形的性质和判定.

练习册系列答案
相关题目
5.已知点A(-2,y1)、B(-1,y2)、C(3,y3)都在反比例函数y=$\frac{3}{2x}$的图象上,则( )
| A. | y1<y2<y3 | B. | y3<y2<y1 | C. | y3<y1<y2 | D. | y2<y1<y3 |
 矩形纸片ABCD的边长AB=4,AD=2.将矩形纸片沿EF折叠,使点A与点C重合,折叠后在其一面着色(如图),则着色部分的面积为多少?
矩形纸片ABCD的边长AB=4,AD=2.将矩形纸片沿EF折叠,使点A与点C重合,折叠后在其一面着色(如图),则着色部分的面积为多少?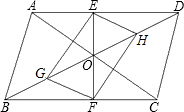 如图,平行四边形ABCD的对角线相交于点O,EF过点O,点G、H分别是OB、OD的中点,四边形EFGH是平行四边形吗?为什么?
如图,平行四边形ABCD的对角线相交于点O,EF过点O,点G、H分别是OB、OD的中点,四边形EFGH是平行四边形吗?为什么? 如图,某飞机在空中飞行的速度是400m/s,着陆前飞行速度与时间的关系成反比例函数,着陆后速度与时间的关系成一次函数关系,从空中到着陆点时间是15s,然后在地面上滑行直至停止,求着陆时飞机的飞行速度是多少?
如图,某飞机在空中飞行的速度是400m/s,着陆前飞行速度与时间的关系成反比例函数,着陆后速度与时间的关系成一次函数关系,从空中到着陆点时间是15s,然后在地面上滑行直至停止,求着陆时飞机的飞行速度是多少?