题目内容
7．
浙江卫视六频道《我老爸最棒》栏目中有一项“大力金刚”的游戏．如图，有6根柱子穿过了一堵木墙，蓝、绿两队的两位老爸分别站在木墙的左、右两侧，需把自己一侧的那段柱子推向对方侧．若每侧每段柱子被选中的机会相等，则两人选到同一根柱子的概率为$\frac{1}{6}$．
分析 先画树状图展示所有36种等可能的结果数，再找出两人选到同一根柱子的结果数，然后根据概率公式求解．
解答 解：6根柱子分别用1、2、3、4、5、6表示，
画树状图为：
共有36种等可能的结果数，其中两人选到同一根柱子的结果数为6，
所以两人选到同一根柱子的概率=$\frac{6}{36}$=$\frac{1}{6}$．
故答案为$\frac{1}{6}$．
点评 本题考查了列表法或树状图法：通过列表法或树状图法展示所有等可能的结果求出n，再从中选出符合事件A或B的结果数目m，然后根据概率公式求出事件A或B的概率．
练习册系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案
相关题目
4．
如图，矩形ABCD中，点B的坐标是（4，3），直线l平行于对角线AC，直线l从原点出发，沿x轴的正方向以每秒1个单位长度运动，与矩形OABC的两边分别交于点M，N，当MN=$\frac{1}{2}$AC时，直线l运动的时间是（ ）
如图，矩形ABCD中，点B的坐标是（4，3），直线l平行于对角线AC，直线l从原点出发，沿x轴的正方向以每秒1个单位长度运动，与矩形OABC的两边分别交于点M，N，当MN=$\frac{1}{2}$AC时，直线l运动的时间是（ ）| A． | 2秒 | B． | 6秒 | C． | 2秒或6秒 | D． | 4秒或8秒 |
18．
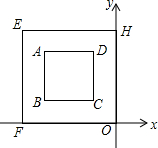如图，在直角坐标系中，正方形EFOH是正方形ABCD经过位似变换得到的，对角线OE=4，则位似中心的坐标是（ ）
如图，在直角坐标系中，正方形EFOH是正方形ABCD经过位似变换得到的，对角线OE=4，则位似中心的坐标是（ ）| A． | （-2，2） | B． | （-$\sqrt{2}$，$\sqrt{2}$） | C． | （-4，4） | D． | （0，0） |
15．已知△ABC的面积是1，A1、B1、C1分别是△ABC三边上的中点，△A1B1C1的面积记为S1；A2、B2、C2分别是△A1B1C1三边上的中点，△A2B2C2的面积记为S2；以此类推，则△A4B4C4的面积S4是（ ）
| A． | $\frac{1}{16}$ | B． | $\frac{1}{64}$ | C． | $\frac{1}{128}$ | D． | $\frac{1}{256}$ |
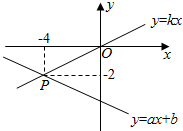如图，已知直线y=ax+b和直线y=kx交于点P（-4，-2），则关于x，y的二元一次方程组$\left\{\begin{array}{l}y=ax+b\\ y=kx\end{array}\right.$的解是$\left\{\begin{array}{l}{x=-4}\\{y=-2}\end{array}\right.$．
已知数a、b、c在数轴上的位置如图所示，化简|a+b|-|a-b|+|a+c|=a-c．