题目内容
18.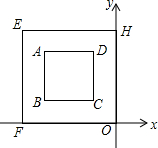 如图,在直角坐标系中,正方形EFOH是正方形ABCD经过位似变换得到的,对角线OE=4,则位似中心的坐标是( )
如图,在直角坐标系中,正方形EFOH是正方形ABCD经过位似变换得到的,对角线OE=4,则位似中心的坐标是( )| A. | (-2,2) | B. | (-$\sqrt{2}$,$\sqrt{2}$) | C. | (-4,4) | D. | (0,0) |
分析 连接OE、HF,交于点M;易得M是位似中心,又由对角线OE=4,M是OE的中点,易得答案.
解答  解:连接OE、HF,交于点M;
解:连接OE、HF,交于点M;
根据题意,在直角坐标系中,正方形EFOH是正方形ABCD经过位似变换得到的,
易得M是位似中心,故M是OE的中点;
又由对角线OE=4,
则E的坐标为(-2$\sqrt{2}$,2$\sqrt{2}$),
M是其中点;
则M的坐标为(-$\sqrt{2}$,$\sqrt{2}$).
故选:B.
点评 本题考查了位似中心的确定,对应点的连线或其连线的反向延长线的交点就是位似中心.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
6. 数x、y在数轴上对应点如图所示,则化简|x+y|-|y-x|的结果是( )
数x、y在数轴上对应点如图所示,则化简|x+y|-|y-x|的结果是( )
 数x、y在数轴上对应点如图所示,则化简|x+y|-|y-x|的结果是( )
数x、y在数轴上对应点如图所示,则化简|x+y|-|y-x|的结果是( )| A. | 0 | B. | 2x | C. | 2y | D. | 2x-2y |
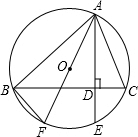 如图,△ABC内接于⊙O,AE⊥BC于D,交⊙O于E,AF为⊙O的直径.
如图,△ABC内接于⊙O,AE⊥BC于D,交⊙O于E,AF为⊙O的直径.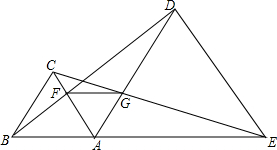 如图,点B、A、E在同一条直线上,△ABC和△ADE是这条直线上方的两个正三角形,连结BD、CE分别交AC、AD于点F、G,连结FG.求证:△AFG是正三角形.
如图,点B、A、E在同一条直线上,△ABC和△ADE是这条直线上方的两个正三角形,连结BD、CE分别交AC、AD于点F、G,连结FG.求证:△AFG是正三角形. 浙江卫视六频道《我老爸最棒》栏目中有一项“大力金刚”的游戏.如图,有6根柱子穿过了一堵木墙,蓝、绿两队的两位老爸分别站在木墙的左、右两侧,需把自己一侧的那段柱子推向对方侧.若每侧每段柱子被选中的机会相等,则两人选到同一根柱子的概率为$\frac{1}{6}$.
浙江卫视六频道《我老爸最棒》栏目中有一项“大力金刚”的游戏.如图,有6根柱子穿过了一堵木墙,蓝、绿两队的两位老爸分别站在木墙的左、右两侧,需把自己一侧的那段柱子推向对方侧.若每侧每段柱子被选中的机会相等,则两人选到同一根柱子的概率为$\frac{1}{6}$.