题目内容
14.直线y=kx+b(k≠0)与抛物线y=ax2(a≠0)的两个交点的横坐标分别是x1和x2,且直线与x轴交点的横坐标是x3,求$\frac{1}{{x}_{1}}$+$\frac{1}{{x}_{2}}$-$\frac{1}{{x}_{3}}$的值.分析 由题意x3=-$\frac{b}{k}$,联立抛物线y=ax2(a>0)与直线y=kx+b得ax2-kx-b=0推出x1+x2=$\frac{k}{a}$,x1x2=-$\frac{b}{a}$,推出 $\frac{1}{{x}_{1}}$+$\frac{1}{{x}_{2}}$=-$\frac{k}{b}$=$\frac{1}{{x}_{3}}$,由此即可得出结论.
解答 解:由题意x3=-$\frac{b}{k}$,联立抛物线y=ax2(a>0)与直线y=kx+b得ax2-kx-b=0,
∴x1+x2=$\frac{k}{a}$,x1x2=-$\frac{b}{a}$,
∴$\frac{1}{{x}_{1}}$+$\frac{1}{{x}_{2}}$=-$\frac{k}{b}$=$\frac{1}{{x}_{3}}$,
∴$\frac{1}{{x}_{1}}$+$\frac{1}{{x}_{2}}$-$\frac{1}{{x}_{3}}$=0.
点评 本题考查抛物线与x轴的交点、一次函数、一元二次方程的根与系数关系等知识,解题的关键是灵活运用所学知识解决问题,体现了数形结合的数学思想.

练习册系列答案
 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
4.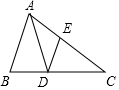 如图,已知AD为△ABC的角平分线,DE∥AB交AC于E,如果$\frac{AE}{EC}$=$\frac{3}{5}$,那么$\frac{AC}{AB}$等于( )
如图,已知AD为△ABC的角平分线,DE∥AB交AC于E,如果$\frac{AE}{EC}$=$\frac{3}{5}$,那么$\frac{AC}{AB}$等于( )
 如图,已知AD为△ABC的角平分线,DE∥AB交AC于E,如果$\frac{AE}{EC}$=$\frac{3}{5}$,那么$\frac{AC}{AB}$等于( )
如图,已知AD为△ABC的角平分线,DE∥AB交AC于E,如果$\frac{AE}{EC}$=$\frac{3}{5}$,那么$\frac{AC}{AB}$等于( )| A. | $\frac{3}{5}$ | B. | $\frac{5}{3}$ | C. | $\frac{8}{5}$ | D. | $\frac{3}{2}$ |
2.果农计划对果园加大种植密度,据测算,果园的总产量y(个)与增种果树的棵数x(棵)间的函数关系式为y=
-5x2+100x+60000,要使总产量在60320个以上,需要增加果树的棵数范围是( )
-5x2+100x+60000,要使总产量在60320个以上,需要增加果树的棵数范围是( )
| A. | 4≤x≤16 | B. | x≥6或x≤16 | C. | 4<x<16 | D. | x>6或x<16 |
6.近似数 3.65×105精确到的数位为( )
| A. | 百分位 | B. | 百位 | C. | 千位 | D. | 万位 |
3.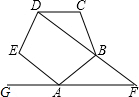 如图,正五边形ABCDE,AF∥CD,交DB的延长线于点F,则∠DFA=( )
如图,正五边形ABCDE,AF∥CD,交DB的延长线于点F,则∠DFA=( )
 如图,正五边形ABCDE,AF∥CD,交DB的延长线于点F,则∠DFA=( )
如图,正五边形ABCDE,AF∥CD,交DB的延长线于点F,则∠DFA=( )| A. | 108° | B. | 72° | C. | 36° | D. | 30° |
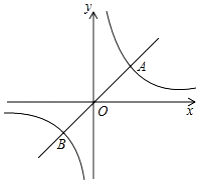 如图,定义:若双曲线y=$\frac{k}{x}$(k>0)与它的其中一条对称轴y=x相交于A、B两点,则线段AB的长度为双曲线y=$\frac{k}{x}$(k>0)的对径.
如图,定义:若双曲线y=$\frac{k}{x}$(k>0)与它的其中一条对称轴y=x相交于A、B两点,则线段AB的长度为双曲线y=$\frac{k}{x}$(k>0)的对径.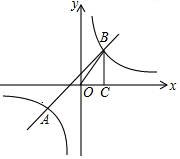 如图,一次函数y1=ax+b与反比例函数y2=$\frac{k}{x}$的图象交于A(m,-2),B(1,n)两点,BC⊥x轴于点C,S△BOC=$\frac{3}{2}$.
如图,一次函数y1=ax+b与反比例函数y2=$\frac{k}{x}$的图象交于A(m,-2),B(1,n)两点,BC⊥x轴于点C,S△BOC=$\frac{3}{2}$. 如图,直线AB、CD相交于点O,OE平分∠AOD,∠DOE=30°,求∠BOC的度数.
如图,直线AB、CD相交于点O,OE平分∠AOD,∠DOE=30°,求∠BOC的度数. 如图,已知点D为等腰直角△ABC内一点,∠CAD=∠CBD=15°,E为AD延长线上的一点,且CE=CA.
如图,已知点D为等腰直角△ABC内一点,∠CAD=∠CBD=15°,E为AD延长线上的一点,且CE=CA.