题目内容
9.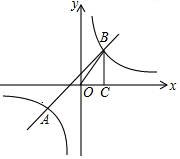 如图,一次函数y1=ax+b与反比例函数y2=$\frac{k}{x}$的图象交于A(m,-2),B(1,n)两点,BC⊥x轴于点C,S△BOC=$\frac{3}{2}$.
如图,一次函数y1=ax+b与反比例函数y2=$\frac{k}{x}$的图象交于A(m,-2),B(1,n)两点,BC⊥x轴于点C,S△BOC=$\frac{3}{2}$.(1)求反比例函数的解析式;
(2)若y1>y2,写出x的取值范围.
分析 (1)根据S△BOC=$\frac{3}{2}$利用反比例函数系数k的几何意义即可得出关于k的一元一次不等式,解之即可得出k值,结合反比例函数图象所在象限即可得出反比例函数解析式;
(2)将y=-2代入反比例函数解析式中求出x值,再根据两函数图象的上下位置关系即可得出不等式的解集.
解答 解:(1)∵BC⊥x轴于点C,点B在反比例函数y2=$\frac{k}{x}$的图象上,
∴S△BOC=$\frac{1}{2}$|k|=$\frac{3}{2}$,
∴k=±3.
∵反比例函数图象在第一、三象限,
∴k=3.
∴反比例函数的解析式为y2=$\frac{3}{x}$.
(2)当y2=$\frac{3}{x}$=-2时,x=m=-$\frac{3}{2}$,
∴点A的坐标为(-$\frac{3}{2}$,-2).
观察函数图象可知:当-$\frac{3}{2}$<x<0或x>1时,一次函数图象在反比例函数图象上方,
∴若y1>y2,x的取值范围为-$\frac{3}{2}$<x<0或x>1.
点评 本题考查了反比例函数与一次函数的交点问题、反比例函数系数k的几何意义以及反比例函数图象上点的坐标特征,解题的关键是:(1)利用反比例函数系数k的几何意义求出k值;(2)利用反比例函数图象上点的坐标特征求出点A的坐标.

练习册系列答案
 一线名师权威作业本系列答案
一线名师权威作业本系列答案
相关题目
19.近似数1.20万精确到( )
| A. | 十分位 | B. | 百分位 | C. | 百位 | D. | 千位 |
17.每天供给地球光和热的太阳与我们的距离非常遥远,它距地球的距离约为15000000千米,将150000000千米用科学记数法表示为( )
| A. | 0.15×109千米 | B. | 1.5×108千米 | C. | 15×107千米 | D. | 1.5×107千米 |
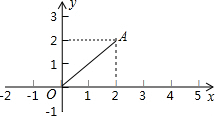 如图,点A的坐标是(2,2),若点P在x轴上,且△APO是等腰三角形,则点P有4个.
如图,点A的坐标是(2,2),若点P在x轴上,且△APO是等腰三角形,则点P有4个.