题目内容
4. 如图,已知点D为等腰直角△ABC内一点,∠CAD=∠CBD=15°,E为AD延长线上的一点,且CE=CA.
如图,已知点D为等腰直角△ABC内一点,∠CAD=∠CBD=15°,E为AD延长线上的一点,且CE=CA.(1)试说明CD垂直于AB;
(2)求证:DE平分∠BDC;
(3)若点M在DE上,且DC=DM,求证:ME=BD.
分析 (1)分别证明D在AB的垂直平分线上,C也在AB的垂直平分线上,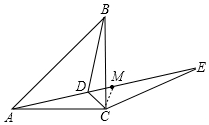 即可解决问题.
即可解决问题.
(2)只要证明∠CDE=∠BDE=60°即可.
(3)首先证明△DCM是等边三角形,再证明△ADC≌△EMC,即可推出ME=AD=BD.
解答 证明:(1)∵△ABC是等腰直角三角形,
∴∠BAC=∠ABC=45°,
∵∠CAD=∠CBD=15°,
∴∠BAD=∠ABD=45°-15°=30°,∠ABD=∠ABC-15°=30°,
∴∠BAD=∠ABD,
∴BD=AD.
∴D在AB的垂直平分线上,
∵AC=BC,
∴C也在AB的垂直平分线上,
∴直线CD是线段AB的垂直平分线.
(2)∵CD是线段AB的垂直平分线,
∴∠ACD=∠BCD=45°,
∴∠CDE=15°+45°=60°,
∴∠BDE=∠DBA+∠BAD=60°,
∴∠CDE=∠BDE,
∴DE平分∠BDC.
(3)如图,连接MC.
∵DC=DM,∠MDC=60°,
∴△DMC是等边三角形.
∴CM=CD,∠DMC=∠CDM=60°,
∴∠ADC=∠EMC=120°,
在△ADC和△EMC中,
$\left\{\begin{array}{l}{∠ADC=∠EMC}\\{∠DAC=∠MEC}\\{AC=EC}\end{array}\right.$,
∴△ADC≌△EMC,
∴ME=AD=BD.
点评 本题考查全等三角形的判定和性质、等腰直角三角形的性质、等边三角形的判定和性质、线段的垂直平分线的判定和性质等知识,解题的关键是灵活运用所学知识解决问题,学会添加常用辅助线,构造全等三角形,属于中考常考题型.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
9.已知点A(m,n)(n≠0)在平面直角坐标系中,则下列各点中,与点关于x轴对称的是( )
| A. | (-m,n) | B. | (m,-n) | C. | (-m,-n) | D. | (n,m) |
16.如图的图形中,既是轴对称图形又是中心对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
13.计算(-18)÷(-3)的结果为( )
| A. | 6 | B. | -6 | C. | 9 | D. | -9 |
 如图,在四边形ABCD中,∠A=90°,AD=3,BC=5,对角线BD平分∠ABC,则△BCD的面积为7.5.
如图,在四边形ABCD中,∠A=90°,AD=3,BC=5,对角线BD平分∠ABC,则△BCD的面积为7.5.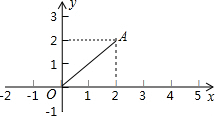 如图,点A的坐标是(2,2),若点P在x轴上,且△APO是等腰三角形,则点P有4个.
如图,点A的坐标是(2,2),若点P在x轴上,且△APO是等腰三角形,则点P有4个.