题目内容
11.在反比例函数y=$\frac{1-3k}{x}$的图象上有两点A(x1,y1)、B(x2,y2).若x1<0<x2,y1<y2则k的取值范围是( )| A. | k≥$\frac{1}{3}$ | B. | k>$\frac{1}{3}$ | C. | k<-$\frac{1}{3}$ | D. | k<$\frac{1}{3}$ |
分析 利用反比例函数的性质得到反比例函数图象分布在第一、三象限,于是得到1-3k>0,然后解不等式即可.
解答 解:∵x1<0<x2,y1<y2,
∴反比例函数图象分布在第一、三象限,
∴1-3k>0,
∴k<$\frac{1}{3}$.
故选D.
点评 本题考查了反比例函数图象上点的坐标特征:反比例函数y=$\frac{k}{x}$(k为常数,k≠0)的图象是双曲线,图象上的点(x,y)的横纵坐标的积是定值k,即xy=k.

练习册系列答案
相关题目
1. 甲、乙两人进行慢跑练习,慢跑路程y(米)与所用时间t(分钟)之间的关系如图所示,下列说法错误的是( )甲、乙两人进行慢跑练习,慢跑路程y(米)与所用时间t(分钟)之间的关系如图所示,下列说法错误的是( )
甲、乙两人进行慢跑练习,慢跑路程y(米)与所用时间t(分钟)之间的关系如图所示,下列说法错误的是( )甲、乙两人进行慢跑练习,慢跑路程y(米)与所用时间t(分钟)之间的关系如图所示,下列说法错误的是( )
 甲、乙两人进行慢跑练习,慢跑路程y(米)与所用时间t(分钟)之间的关系如图所示,下列说法错误的是( )甲、乙两人进行慢跑练习,慢跑路程y(米)与所用时间t(分钟)之间的关系如图所示,下列说法错误的是( )
甲、乙两人进行慢跑练习,慢跑路程y(米)与所用时间t(分钟)之间的关系如图所示,下列说法错误的是( )甲、乙两人进行慢跑练习,慢跑路程y(米)与所用时间t(分钟)之间的关系如图所示,下列说法错误的是( )| A. | 前2分钟,乙的平均速度比甲快 | |
| B. | 甲、乙两人8分钟各跑了800米 | |
| C. | 5分钟时两人都跑了500米 | |
| D. | 甲跑完800米的平均速度为100米/分 |
2.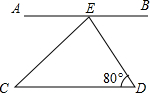 如图,AB∥CD,CE平分∠AED,则∠C=( )
如图,AB∥CD,CE平分∠AED,则∠C=( )
 如图,AB∥CD,CE平分∠AED,则∠C=( )
如图,AB∥CD,CE平分∠AED,则∠C=( )| A. | 40° | B. | 45° | C. | 50° | D. | 55° |
19.若x是3的相反数,|y|=4,则x-y的值是( )
| A. | -7 | B. | 1 | C. | -1或7 | D. | 1或-7 |
16.下列实数中,属于无理数的是( )
| A. | -3 | B. | 3.14 | C. | $\frac{2}{7}$ | D. | $\sqrt{2}$ |
3.下列计算正确的是( )
| A. | a2•a=2a3 | B. | a2•a3=2a6 | C. | (-2a3)2=4a6 | D. | a8÷a2=a4 |
20.平面直角坐标系xOy中,⊙A的半径为5,点A的坐标为(2,1),点P的坐标为(0,6),则点P与⊙A的位置关系是( )
| A. | 点P在⊙A外 | B. | 点P在⊙A上 | C. | 点P在⊙A内 | D. | 不能确定 |
1.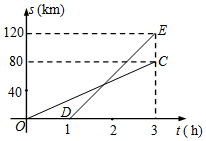 已知A,B两地相距80km,甲,乙两人沿同一条公路从A地出发到B地,乙骑自行车,甲骑摩托车.图中DE,OC分别表示甲,乙离开A地的路程s(km)与时间t(h)的函数关系,根据图象得出的下列信息错误的是( )
已知A,B两地相距80km,甲,乙两人沿同一条公路从A地出发到B地,乙骑自行车,甲骑摩托车.图中DE,OC分别表示甲,乙离开A地的路程s(km)与时间t(h)的函数关系,根据图象得出的下列信息错误的是( )
 已知A,B两地相距80km,甲,乙两人沿同一条公路从A地出发到B地,乙骑自行车,甲骑摩托车.图中DE,OC分别表示甲,乙离开A地的路程s(km)与时间t(h)的函数关系,根据图象得出的下列信息错误的是( )
已知A,B两地相距80km,甲,乙两人沿同一条公路从A地出发到B地,乙骑自行车,甲骑摩托车.图中DE,OC分别表示甲,乙离开A地的路程s(km)与时间t(h)的函数关系,根据图象得出的下列信息错误的是( )| A. | 乙到达B地时甲距A地120km | B. | 乙出发1.8小时被甲追上 | ||
| C. | 甲,乙相距20km时,t为2.4h | D. | 甲的速度是乙的速度的$\frac{9}{4}$倍 |