题目内容
1.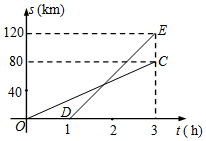 已知A,B两地相距80km,甲,乙两人沿同一条公路从A地出发到B地,乙骑自行车,甲骑摩托车.图中DE,OC分别表示甲,乙离开A地的路程s(km)与时间t(h)的函数关系,根据图象得出的下列信息错误的是( )
已知A,B两地相距80km,甲,乙两人沿同一条公路从A地出发到B地,乙骑自行车,甲骑摩托车.图中DE,OC分别表示甲,乙离开A地的路程s(km)与时间t(h)的函数关系,根据图象得出的下列信息错误的是( )| A. | 乙到达B地时甲距A地120km | B. | 乙出发1.8小时被甲追上 | ||
| C. | 甲,乙相距20km时,t为2.4h | D. | 甲的速度是乙的速度的$\frac{9}{4}$倍 |
分析 根据题意和函数图象中的数据可以计算出出各个选项中的量,从而可以判断各个选项是否正确,从而可以解答本题.
解答 解:由题意和图象可得,
乙到达B地时甲距A地120km,故选项A正确,
甲的速度是:120÷(3-1)=60km/h,乙的速度是:80÷3=$\frac{80}{3}$km/h,
则甲的速度是乙的速度的:$\frac{60}{\frac{80}{3}}=\frac{9}{4}$倍,故选项D正确,
设乙出发后被甲追上的时间为xh,则60(x-1)=$\frac{80}{3}x$,得x=1.8,故选项B正确,
由图象可知,甲乙相距20km时的时间有两个时刻,一个是相遇之前,一个是相遇之后,故选项C错误,
故选C.
点评 本题考查函数的图象,解答本题的关键是明确题意,找出所求问题需要的条件,利用数形结合的思想解答.

练习册系列答案
相关题目
11.在反比例函数y=$\frac{1-3k}{x}$的图象上有两点A(x1,y1)、B(x2,y2).若x1<0<x2,y1<y2则k的取值范围是( )
| A. | k≥$\frac{1}{3}$ | B. | k>$\frac{1}{3}$ | C. | k<-$\frac{1}{3}$ | D. | k<$\frac{1}{3}$ |
12.在平面直角坐标系中,点A(4,-2),B(0,2),C(a,-a),a为实数,当△ABC的周长最小时,a的值是( )
| A. | -1 | B. | 0 | C. | 1 | D. | $\sqrt{2}$ |
9.在下列四个汽车标志图案中,是中心对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
16. 如图,已知a∥b,∠1=68°,则∠2=( )
如图,已知a∥b,∠1=68°,则∠2=( )
 如图,已知a∥b,∠1=68°,则∠2=( )
如图,已知a∥b,∠1=68°,则∠2=( )| A. | 22° | B. | 68° | C. | 102° | D. | 112° |
6.下列所述图形中,既是中心对称图形,又是轴对称图形的是( )
| A. | 平行四边形 | B. | 菱形 | C. | 正三角形 | D. | 正五边形 |
13.将抛物线y=(x-1)2+4先向右平移4个单位长度,再向下平移3个单位长度,得到的抛物线的顶点坐标为( )
| A. | (5,4) | B. | (1,4) | C. | (1,1) | D. | (5,1) |
10.若 x2-2(m-1)x+9 是完全平方式,则m的值为( )
| A. | 4 | B. | 2或-4 | C. | ±6 | D. | -2或4 |