题目内容
12.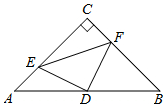 如图,在△ABC中,∠C=90°,AC=BC=4,D是AB的中点,点E、F分别在AC、BC边上运动(点E不与点A、C重合),且保持AE=CF,连接DE、DF、EF.在此运动变化的过程中,有下列结论:①△DFE是等腰直角三角形;②四边形CEDF不可能为正方形;③四边形CEDF的面积随点E位置的改变而发生变化;④点C、E、D、F四点在同一个圆上,且该圆的面积最小为4π.其中错误结论的个数是( )个.
如图,在△ABC中,∠C=90°,AC=BC=4,D是AB的中点,点E、F分别在AC、BC边上运动(点E不与点A、C重合),且保持AE=CF,连接DE、DF、EF.在此运动变化的过程中,有下列结论:①△DFE是等腰直角三角形;②四边形CEDF不可能为正方形;③四边形CEDF的面积随点E位置的改变而发生变化;④点C、E、D、F四点在同一个圆上,且该圆的面积最小为4π.其中错误结论的个数是( )个.| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
分析 ①正确.连接CD.只要证明△ADE≌△CDF(SAS),即可解决问题.
②错误.当E、F分别为AC、BC中点时,四边形CEDF为正方形.
③错误.四边形CEDF的面积=$\frac{1}{2}$S△ABC=$\frac{1}{2}$×$\frac{1}{2}$×4×4=4,为定值.
④错误.以EF为直径的圆的面积的最小值=π•( $\frac{1}{2}$•2 $\sqrt{2}$)2=2π.
解答 解:连接CD,如图1,
∵∠C=90°,AC=BC=4,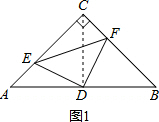
∵△ABC是等腰直角三角形,
∴∠A=∠B=45°,
∵D为AB的中点,
∴CD⊥AB,CD=AD=BD,
∴∠DCB=∠B=45°,
∴∠A=∠DCF,
在△ADE和△CDF中
$\left\{\begin{array}{l}{AE=CF}\\{∠A=∠DCF}\\{AD=CD}\end{array}\right.$,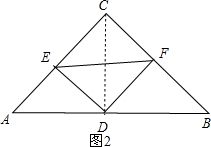
∴△ADE≌△CDF(SAS),
∴ED=DF,∠CDF=∠ADE,
∵∠ADE+∠EDC=90°,
∴∠EDC+∠CDF=90°,即∠EDF=90°,
∴△DFE是等腰直角三角形,所以①正确;
当E、F分别为AC、BC中点时,如图2,则AE=CE=CF=BF,DE=AE=CE,
∴CE=CF=DE=DF,
而∠ECF=90°,
∴四边形CDFE是正方形,所以②错误;
∵△ADE≌△CDF,
∴S△ADE=S△CDF,
∴S四边形CEDF=S△CDE+S△CDF=S△CDE+S△ADE=S△ADC=$\frac{1}{2}$S△ABC=$\frac{1}{2}$×$\frac{1}{2}$×4×4=4,所以③错误;
∵△CEF和△DEF都为直角三角形,
∴点C、D在以EF为直径的圆上,即点C、E、D、F四点在同一个圆上,
∵△DEF是等腰直角三角形,
∴EF=$\sqrt{2}$DE,
当DE⊥AC时,DE最短,此时DE=$\frac{1}{2}$AC=2,
∴EF的最小值为2 $\sqrt{2}$,
∴以EF为直径的圆的面积的最小值=π•( $\frac{1}{2}$•2 $\sqrt{2}$)2=2π,所以④错误;
故选C.
点评 本题考查三角形的综合题、等腰直角三角形的判定与性质、直角三角形斜边上的中线性质、全等三角形的判定和性质等知识,解题的关键是学会添加常用辅助线,构造全等三角形解决问题,属于中考压轴题.

 优化作业上海科技文献出版社系列答案
优化作业上海科技文献出版社系列答案| A. | 点P的⊙O外 | B. | 点P的⊙O上 | C. | 点P的⊙O内 | D. | 无法确定 |
| 价目表 | |
| 不超过200度的部分 | 0.50元/度 |
| 超过200度不超过400度的部分 | a元/度 |
| 超过400度的部分 | 0.80元/度 |
| 注:电费按月结算 | |
(2)某户居民10月份用电220度,应缴电费111元,求a的值;
(3)用x(度)表示月用电量,请根据x的不同取值范围用含x的代数式表示该月应缴电费.
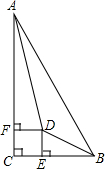 已知:如图,在Rt△ABC中,∠C=90°,∠BAC、∠ABC的平分线相交于点D,DE⊥BC,DF⊥AC,垂足分别为E、F.求证:四边形CEDF是正方形.
已知:如图,在Rt△ABC中,∠C=90°,∠BAC、∠ABC的平分线相交于点D,DE⊥BC,DF⊥AC,垂足分别为E、F.求证:四边形CEDF是正方形.
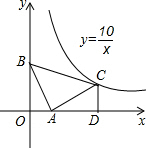 如图,在等腰直角三角形ABC中,∠BAC=90°,点A在x轴上,点B的坐标是(0,3).若点C恰好在反比例函数y=$\frac{10}{x}$第一象限内的图象上,过点C作CD⊥x轴于点D,那么点C的坐标为(5,2).
如图,在等腰直角三角形ABC中,∠BAC=90°,点A在x轴上,点B的坐标是(0,3).若点C恰好在反比例函数y=$\frac{10}{x}$第一象限内的图象上,过点C作CD⊥x轴于点D,那么点C的坐标为(5,2).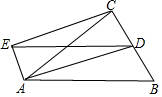 如图,在△ABC中,AB=AC,D为BC的中点,点E是△ABC外一点且四边形ABDE是平行四边形.
如图,在△ABC中,AB=AC,D为BC的中点,点E是△ABC外一点且四边形ABDE是平行四边形.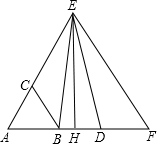 如图,已知D是等边三角形ABC的AB边延长线上一点,BD的垂直平分线HE交AC延长线于点E,那么CE与AD相等吗?试说明理由.
如图,已知D是等边三角形ABC的AB边延长线上一点,BD的垂直平分线HE交AC延长线于点E,那么CE与AD相等吗?试说明理由.