题目内容
 已知,如图,在?ABCD中,AD⊥BD,点E,F分别在AB,BD上,且满足AD=AE=DF,连接DE,AF,EF.
已知,如图,在?ABCD中,AD⊥BD,点E,F分别在AB,BD上,且满足AD=AE=DF,连接DE,AF,EF.(1)若∠CDB=20°,求∠EAF的度数.
(2)若DE⊥EF,求证:DE=2EF.
考点:平行四边形的性质
专题:
分析:(1)由在?ABCD中,AD⊥BD,∠CDB=20°,即可求得∠DAB的度数,又由AD=DF,即可求得∠DAF的度数,继而求得答案;
(2)首先过点A作AM⊥DE于M,易证得△ADM≌△DFE,然后由等腰三角形的性质,即可证得结论.
(2)首先过点A作AM⊥DE于M,易证得△ADM≌△DFE,然后由等腰三角形的性质,即可证得结论.
解答:解:(1)∵四边形ABCD是平行四边形,
∴AB∥CD,
∵AD⊥BD,∠CDB=20°,
∵∠ADC=∠ADB+∠CDB=110°,
∴∠DAB=180°-∠ADC=70°,
∵AD=DF,
∴∠DAF=∠DFA=45°,
∴∠EAF=∠DAB-∠DAF=25°;
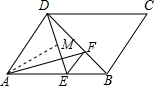 (2)过点A作AM⊥DE于M,
(2)过点A作AM⊥DE于M,
∵DE⊥EF,
∴∠AMD=∠DEF=90°,
∵∠ADM+∠EDF=90°,∠EDF+∠DFE=90°,
∴∠ADM=∠DFE,
在△ADM和△DFE中,
,
∴△ADM≌△DFE(AAS),
∴DM=EF,
∵AD=AE,
∴DE=2DM=2EF.
∴AB∥CD,
∵AD⊥BD,∠CDB=20°,
∵∠ADC=∠ADB+∠CDB=110°,
∴∠DAB=180°-∠ADC=70°,
∵AD=DF,
∴∠DAF=∠DFA=45°,
∴∠EAF=∠DAB-∠DAF=25°;
 (2)过点A作AM⊥DE于M,
(2)过点A作AM⊥DE于M,∵DE⊥EF,
∴∠AMD=∠DEF=90°,
∵∠ADM+∠EDF=90°,∠EDF+∠DFE=90°,
∴∠ADM=∠DFE,
在△ADM和△DFE中,
|
∴△ADM≌△DFE(AAS),
∴DM=EF,
∵AD=AE,
∴DE=2DM=2EF.
点评:此题考查了平行四边形的性质、等腰直角三角形的性质以及全等三角形的判定与性质.此题比较适中,注意掌握辅助线的作法,注意掌握数形结合思想的应用.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
下列各说法中,正确的是( )
| A、全等图形是指性状相同的两个图形 |
| B、全等三角形是指面积相同的两个三角形 |
| C、等边三角形都是全等三角形 |
| D、全等图形的周长、面积相等 |
| E、全等图形是指性状相同的两个 |
小于
的所有非负整数和是( )
| 19 |
| 6 |
| A、-6 | B、0 | C、6 | D、19 |
 如图,已知⊙O的半径为
如图,已知⊙O的半径为 已知AB∥CD,求证:∠A=∠E+∠C.
已知AB∥CD,求证:∠A=∠E+∠C.