Question

1．如图，在四边形ABCD中，AD∥BC，E为CD中点，AE平分∠BAD，有下列结论：
①AD+BC=AB；②AE⊥BE；③以AB为直径的圆与CD相切；④若以CD为直径的圆与AB相切，则以AB为直径的圆也与CD相切．其中正确的是①②（把所有正确结论的序号都选上）

Answer 1

分析 延长AE交BC于F，如图，利用平行线的性质得∠DAE=∠F，加上∠DAE=∠BAE，则∠F=∠BAE，所以BA=BF，再利用“AAS”证明△ADE≌△FCE得到AD=CF，AE=EF，则可对①正进行判断；根据等腰三角形的性质可对②进行判断；取AB的中点P，连接PE，如图，利用梯形中位线性质得PE=$\frac{1}{2}$（AD+BC）=PA，PE∥AD，由于CD与AD不一定垂直，则PE与CD不一定垂直，则根据切线的判定方法对③进行判断；作EH⊥AB于H，当以CD为直径的圆与AB相切时，根据切线的性质得EH=ED，由于不能得到∠D=90°，所以不能判断以AB为直径的圆也与CD相切．则可对④进行判断．

解答 解：延长AE交BC于F，如图，
∵AD∥BC，
∴∠DAE=∠F，
∵AE平分∠BAD
∴∠DAE=∠BAE，
∴∠F=∠BAE，
∴BA=BF，
∵E为CD中点，
∴DE=CE，
在△ADE和△FCE中
$\left\{\begin{array}{l}{∠DAE=∠F}\\{∠AED=∠FEC}\\{DE=CE}\end{array}\right.$
∴△ADE≌△FCE，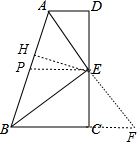
∴AD=CF，AE=EF，
∴BA=BF=BC+CF=BC+AD，所以①正确；
∵BA=BF，AE=EF，
∴BE⊥AF，所以②正确；
取AB的中点P，连接PE，如图，
∴PE=$\frac{1}{2}$（AD+BC）=$\frac{1}{2}$•AB=PA，PE∥AD
而CD与AD不一定垂直，
∴PE与CD不一定垂直，
∴以AB为直径的圆与CD不一定相切，所以③错误；
作EH⊥AB于H，
当以CD为直径的圆与AB相切时，则EH=ED，虽然∠DAE=∠HAE，AE为公共边，不能证明△EAH与△EAD全等，不能得到∠D=90°，所以不能判断以AB为直径的圆也与CD相切．所以④错误．
故答案为①②．

点评 本题考查了切线的判定与性质：圆的切线垂直于经过切点的半径；经过半径的外端且垂直于这条半径的直线是圆的切线．判定切线时“连圆心和直线与圆的公共点”或“过圆心作这条直线的垂线”；有切线时，常常“遇到切点连圆心得半径．也考查了平行线的性质．