题目内容
4.根据国家精准扶贫政策,某地A、B两局分别提供12个和6个扶贫名额,甲、乙两地分别有贫苦户10户、8户,其中A局每个名额给甲、乙两地的钱数分别为400元、800元,B局每个名额给甲、乙两地的钱数分别为300元、500元(1)设B局给甲地x个名额,求总钱数y关于x的关系式;
(2)若总钱数不超过9000元,问共有几种分配方案.
分析 (1)根据总钱数=A局给甲、乙两地的钱数+B局给甲、乙两地的钱数,从而得到总钱数y关于x的关系式;
(2)根据总钱数不超过9000元可得不等式,解不等式可得共有几种分配方案.
解答 解:(1)依题意有
y=400(10-x)+800(12-10+x)+300x+500(6-x)=200x+8600.
故总钱数y关于x的关系式为y=200x+8600;
(2)依题意有
200x+8600≤9000,
解得x≤2,
∵x为正整数,
∴共有2种分配方案:
①A局给甲地8个名额、乙地4个名额,B局给甲地2个名额、乙地4个名额;
②A局给甲地9个名额、乙地3个名额,B局给甲地1个名额、乙地5个名额.
点评 考查了一元一次不等式的应用,函数关系式,解决问题的关键是读懂题意,找到关键描述语,找到所求的量的等量关系和不等关系.

练习册系列答案
相关题目
4.当a≠0时,下列运算正确的是( )
| A. | a0=0 | B. | ${a^{-2}}=-\frac{1}{a^2}$ | C. | (-a)4=-a4 | D. | a-2÷a-3=a |
5.下列等式不成立的是( )
| A. | $\sqrt{2}$+$\sqrt{3}$=$\sqrt{5}$ | B. | $\sqrt{8}$-$\sqrt{2}$=$\sqrt{2}$ | C. | $\sqrt{2}$×$\sqrt{3}$=$\sqrt{6}$ | D. | $\frac{1}{\sqrt{5}}$=$\frac{\sqrt{5}}{5}$ |
2.已知三角形两边的长分别是4和10,则此三角形第三边的长可能是( )
| A. | 5 | B. | 6 | C. | 9 | D. | 15 |
9.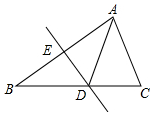 如图,将△ABC沿直线DE折叠后,使得点B与点A重合,已知AC=10cm,△ADC的周长为34cm,则BC的长为( )
如图,将△ABC沿直线DE折叠后,使得点B与点A重合,已知AC=10cm,△ADC的周长为34cm,则BC的长为( )
 如图,将△ABC沿直线DE折叠后,使得点B与点A重合,已知AC=10cm,△ADC的周长为34cm,则BC的长为( )
如图,将△ABC沿直线DE折叠后,使得点B与点A重合,已知AC=10cm,△ADC的周长为34cm,则BC的长为( )| A. | 14cm | B. | 20cm | C. | 44cm | D. | 24cm |
14.如图,BF、CF分别是∠DBC和∠ECB的角平分线,则关于F的说法不正确的是( )
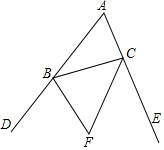

| A. | F到△ABC三边所在直线的距离相等 | B. | F在∠A的平分线上 | ||
| C. | F到△ABC三顶点的距离相等 | D. | F到BD、CE的距离相等 |