题目内容
9.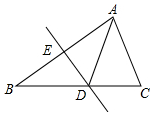 如图,将△ABC沿直线DE折叠后,使得点B与点A重合,已知AC=10cm,△ADC的周长为34cm,则BC的长为( )
如图,将△ABC沿直线DE折叠后,使得点B与点A重合,已知AC=10cm,△ADC的周长为34cm,则BC的长为( )| A. | 14cm | B. | 20cm | C. | 44cm | D. | 24cm |
分析 首先根据折叠的性质可得AD=BD,再由△ADC的周长为34cm可以得到AD+DC的长,利用等量代换可得BC的长.
解答 解:∵将△ABC沿直线DE折叠后,使得点B与点A重合,
∴AD=BD,
∵△ADC的周长为34cm,AC=10cm,
∴AD+DC=34-10=24(cm),
∵AD=BD,
∴BD+DC=24cm,即BC=24cm.
故选:D.
点评 此题主要考查了翻折变换,关键是掌握折叠是一种对称变换,它属于轴对称,折叠前后图形的形状和大小不变,位置变化,对应边和对应角相等.

练习册系列答案
相关题目
19.下列各组数据中的三个数作为三角形的边长,其中能构成直角三角形的是( )
| A. | 1,2,3 | B. | $\sqrt{2}$,$\sqrt{3}$,$\sqrt{5}$ | C. | 3,5,7 | D. | 5,7,9 |
20.在△ABC中,∠C=90°,AC=4,AB=5,以点C为圆心,以R长我半径画圆,若⊙C与边AB只有一个公共点,则R的取值范围是( )
| A. | R=$\frac{12}{5}$ | B. | 3≤R≤4 | C. | 0<R<3或R>4 | D. | 3<R≤4或R=$\frac{12}{5}$ |
17.计算:(-2)-5=( )
| A. | 3 | B. | -3 | C. | -7 | D. | 7 |
11.在2,-$\frac{5}{2}$,0,-2.3中最小的有理数是( )
| A. | $-\frac{5}{2}$ | B. | -2.3 | C. | 2 | D. | 0 |
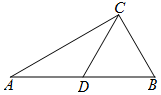 如图,在△ABC中,∠ACB=90°,点D是AB的中点,过点D作DE⊥AC于点E,
如图,在△ABC中,∠ACB=90°,点D是AB的中点,过点D作DE⊥AC于点E,